pola trójkątów Krystek: cześć, mam zadanie którego nie wiem jak rozwiazać Dany jest trójkąt prostokątny ABC, w kórym kąt BAC=90 stopni oraz |AC|=12 cm. Na boku AB tego trójkąta zaznaczono punkt E w taki sposób, że |CE|=|EB|. wiedząc, że pole trójkąta ABC jest róne 108 cm kwadratowych, oblicz: a) pole trójkąta BCE b)wysokość trójkąta BCE poprowadzoną z punktu E

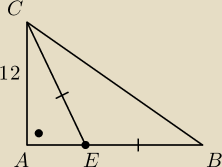
Adamm: P_ABC=108 |EB|=x, |AE|=h

	1
PABC=12*		*(x+h)
	2

h=√x²−12² 6(x+√x²−144)=108 x+√x²−144=18 √x²−144=18−x x²−144=324−36x+x² 36x=468 x=13

	1
PBCE=12*		*13=78
	2

Krystek: A wysokość jak można policzyć?

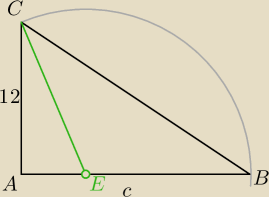
Tadeusz: 108=6c ⇒ c=18 itd

Krystek: Obliczyć przeciwprostokatna i do wzoru na pole z którego oblicze h, tak? A nie ma jnnego sposobu na rozwiązanie tego zadania?

Adamm: |CB|=√12²+(5+13)²=√468=6√13

	1
PBCE=		*|CB|*hE=3√13*hE=78
	2

h_E=2√13

Adamm: pewnie jest, ale wymyślić musisz go już sam

Krystek: można do czegoś wykorzystać fakt że wartość sinα AEC i BEC są takie same?

Krystek: Up

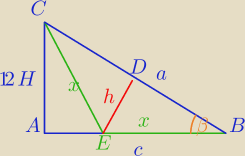
Mila: P_ΔABC=108

	1
108=		c*h
	2

	1
108=		*c*12
	2

c=108:6=18 a²=12²+18² a²=144+324=468 a=√468=√4*9*13=6√13 |DB|=3√13 W ΔBAC:

	18		3
cosβ=		=
	6√13		√13

W ΔBDE:

	|DB|
cosβ=		⇔
	x

3		3√3
	=		⇔ x=13
√13		x

13²=h²+(3√13)² h²=169−9*13=169−117 h²=52 h=2√13

	1
PΔBCE=		*6√13*2√13=78
	2

a)P_ΔBCE=78 b) h=2√13