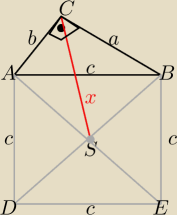
 Korzystając z rysunku
ABDE to kwadrat zbudowany na przeciwprostokątnej c
wykaż ,że x=√2(R+r)
gdzie R i r są odpowiednio długościami promieni okręgu opisanego i wpisanego w trójkąt ABC
Korzystając z rysunku
ABDE to kwadrat zbudowany na przeciwprostokątnej c
wykaż ,że x=√2(R+r)
gdzie R i r są odpowiednio długościami promieni okręgu opisanego i wpisanego w trójkąt ABC
 1) Na czworokącie ASBC można opisać okrąg − Sumy miar kątów przeciwległych są równe 180o.
Korzystając z tw. Ptolemeusza:
c*x=b*|SB|+a*|AS|⇔
1) Na czworokącie ASBC można opisać okrąg − Sumy miar kątów przeciwległych są równe 180o.
Korzystając z tw. Ptolemeusza:
c*x=b*|SB|+a*|AS|⇔
| c√2 | c√2 | |||
c*x=b* | +a* | ⇔ | ||
| 2 | 2 |
| √2 | ||
x= | *(a+b) | |
| 2 |
| √2 | ||
3) x= | *(2R+2r)⇔ | |
| 2 |
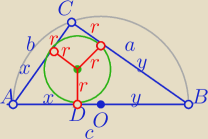 ΔABC− Δprostokątny.
ΔABC− Δprostokątny.
| 1 | ||
R= | c − promień okręgu opisanego na ΔABC | |
| 2 |

 Eta .... m jeszcze nie za bardzo
Eta .... m jeszcze nie za bardzo 




