Mila:
1) jeżeli funkcja różniczkowalna w przedziale osiąga w pewnym punkcie wewnętrznym x
0 tego
przedziału ekstremum lokalne, to pochodna w tym punkcie f'(x
0)=0.
2)
Twierdzenie odwrotne nie jest prawdziwe.
Przykład.
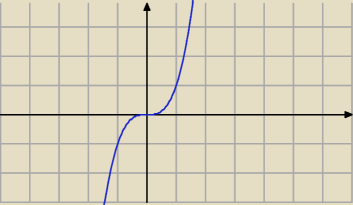
f(x)=x
3
f'(x)=3x
2
f'(x)=0⇔3x
2=0⇔x=0 jednak w punkcie x=0 ta funkcja nie posiada ekstremum . Patrz wykres:
( ta funkcja w punkcie x=0 ma punkt przegięcia )
3) Jeżeli pierwsza pochodna f'(x) :
dla x<x
0 jest ujemna (dodatnia)
f'(x
0)=0
dla x>x
0 jest dodatnia (ujemna) to posiada w x
0 ekstremum.
Słownie wyrazimy tak: pierwsza pochodna przy przejściu zmiennej przez punkt x
0 zmienia znak ,
z ujemnego na dodatni to f(x) ma w x0 ekstremum− minimum,
jeżeli f'(x) przy przejściu zmiennej przez punkt x
0 zmienia znak
z dodatniego na ujemny to f(x) ma w x0 ekstremum− maksimum
4) Krótko: funkcja
różniczkowalna ma w x
0 ekstremum wtedy i tylko wtedy gdy
f'(x)=0 i i pochodna zmienia znak przy przejściu przez punkt x
0.


 1) jeżeli funkcja różniczkowalna w przedziale osiąga w pewnym punkcie wewnętrznym x0 tego
przedziału ekstremum lokalne, to pochodna w tym punkcie f'(x0)=0.
2)
Twierdzenie odwrotne nie jest prawdziwe.
Przykład.
f(x)=x3
f'(x)=3x2
f'(x)=0⇔3x2=0⇔x=0 jednak w punkcie x=0 ta funkcja nie posiada ekstremum . Patrz wykres:
( ta funkcja w punkcie x=0 ma punkt przegięcia )
3) Jeżeli pierwsza pochodna f'(x) :
dla x<x0 jest ujemna (dodatnia)
f'(x0)=0
dla x>x0 jest dodatnia (ujemna) to posiada w x0 ekstremum.
Słownie wyrazimy tak: pierwsza pochodna przy przejściu zmiennej przez punkt x0 zmienia znak ,
z ujemnego na dodatni to f(x) ma w x0 ekstremum− minimum,
jeżeli f'(x) przy przejściu zmiennej przez punkt x0 zmienia znak
z dodatniego na ujemny to f(x) ma w x0 ekstremum− maksimum
4) Krótko: funkcja różniczkowalna ma w x0 ekstremum wtedy i tylko wtedy gdy
f'(x)=0 i i pochodna zmienia znak przy przejściu przez punkt x0.
1) jeżeli funkcja różniczkowalna w przedziale osiąga w pewnym punkcie wewnętrznym x0 tego
przedziału ekstremum lokalne, to pochodna w tym punkcie f'(x0)=0.
2)
Twierdzenie odwrotne nie jest prawdziwe.
Przykład.
f(x)=x3
f'(x)=3x2
f'(x)=0⇔3x2=0⇔x=0 jednak w punkcie x=0 ta funkcja nie posiada ekstremum . Patrz wykres:
( ta funkcja w punkcie x=0 ma punkt przegięcia )
3) Jeżeli pierwsza pochodna f'(x) :
dla x<x0 jest ujemna (dodatnia)
f'(x0)=0
dla x>x0 jest dodatnia (ujemna) to posiada w x0 ekstremum.
Słownie wyrazimy tak: pierwsza pochodna przy przejściu zmiennej przez punkt x0 zmienia znak ,
z ujemnego na dodatni to f(x) ma w x0 ekstremum− minimum,
jeżeli f'(x) przy przejściu zmiennej przez punkt x0 zmienia znak
z dodatniego na ujemny to f(x) ma w x0 ekstremum− maksimum
4) Krótko: funkcja różniczkowalna ma w x0 ekstremum wtedy i tylko wtedy gdy
f'(x)=0 i i pochodna zmienia znak przy przejściu przez punkt x0.