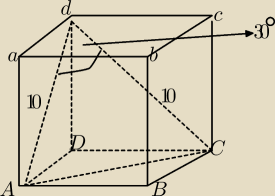
pomocy kajka: Podstawą prostopadłościanu jest kwadrat o boku a. Przekątne sąsiednich ścian bocznych, wychodzących z jednego wierzchołka, tego prostopadłościanu mają dlugośc 10 i tworzą ramiona kąta o mierze 30. oblicz: a)pole przekroju prostopadłościanu płaszczyzną poprowadzoną przez przekątną podstawy i przeciwległy wierzchołek górnej podstawy b)oblicz krawędzi tego prostopadłościanu

	√6−√2		√6+√2
W obliczeniach przyjmij sin15°=cos75°=		, cos15°=sin75°=
	4		4

i czy mółyby mi ktoś to rozwiązać bo tego nie rozumiem

Mila: Twierdzenie cosinusów znasz? Czy jeszcze nie było na lekcjach?

kajka: Znam

kajka:

kajka: Znam

Janek191: Lepiej tw. kosinusów

Janek191: I AC I = x

	√3
x2 = 102 + 102 − 2*10*10 *cos 30o = 100 + 100 − 200*		= 200 − 100√3
	2

x² = 100*( 2 −√3) x = 10 √2 − √3 =============

kajka: Dziękuję i jak dalej ?

Janek191: Teraz oblicz wysokość równoramiennego Δ ACD − tw Pitagorasa

Janek191: h² = 10² − ( 5 √2 −√3)²

kajka: Ok

Janek191: Lub

h		√6 + √2
	= sin 75o =
10		4

	√6 + √2
h = 10*		=
	4

Janek191: P_{Δ ACD} = 0,5 x*h

Janek191:

0,5 x		√6 − √2
	= cos 75o =		/ *2
10		4

x		√6 − √2
	=
10		2

x = 5*( √6 − √2) =============