mat
Paweł:
Skoro n√z = {Z0, Z1, ..., Zn−1} to czy
3√1 zapisuje się jako {10, 11, 12}?
22 paź 18:50
Janek191:
Zapisujemy:
z0, z1, z2
22 paź 18:52
Paweł: Więc będzie 3√1 = {Z0, Z1, Z2}?
22 paź 18:53
Janek191:
Oblicz : z
0, z
1, z
2 
22 paź 19:47
Paweł:
Właśnie tak nad tym myślę.
Póki co podstawiłem pod wzór i od dłuższego czasu myślę co dalej.
Będę wdzięczny za wskazówki

| | α | | α | |
Z0 = 3√r(cos |
| + isin |
| ) |
| | 3 | | 3 | |
| | α + 2π | | α + 2π | |
Z1 = 3√r(cos |
| + isin |
| ) |
| | 3 | | 3 | |
| | α + 4π | | α + 4π | |
Z2 = 3√r(cos |
| + isin |
| ) |
| | 3 | | 3 | |
Wyglądałoby na to, że potrzebuję wartości r oraz α..
22 paź 19:54
Janek191:
1 = cos 0 + i sin 0
więc
α = 0
22 paź 19:55
Janek191:
r = 1
22 paź 19:55
PW: r to odległość liczby (a,b) od (0,0), a więc tutaj r = 1, bo odległość liczby (1, 0) od (0, 0)
wynosi 1.
α = 0, bo 1 = cos0 + i sin0.
22 paź 20:00
Paweł:
| | 1 | | √3 | |
Więc jakby liczyć nie z 1 a z np. √2 to α=45, albo z |
| + |
| to α=30? |
| | 2 | | 2 | |
Pytanie jeszcze dlaczego r = 1?
Moja wiedza dot r ogranicza się do znajomości wzoru i interpretacji geometrycznej:
r = |z| =
√x2 + y2
22 paź 20:03
Paweł:
PW − dla pewności zapytam: tutaj liczyłem z=1 czyli zespoloną, która nie ma części urojonej, a
więc r = |Re(z)|?
Jakbym miał np. 3+2i to byłoby r = √32 + 22 = √13?
22 paź 20:08
cds:
22 paź 20:08
5-latek: Pierwiastki stopnia trezeciego z jednosci mozna policzyc z postaci trygonometrycznej ale
rozmiez rozwiazujac rownie z
3=1
Dostaniemy wtedy
ω
0=1
Warto znacna pamiec te wartosci bo bardzo czesto sie przydaja
Bo np chcac obliczyc p3{8] to wiesz ze jednym z pierwiastkow jest u
0= 2 to u
1= 2*ω
1 i
u
2= 2*ω
2
Nie trzeba wtedy tak duzo sie oliczyc .
22 paź 20:11
Janek191:
Tak

22 paź 20:11
Paweł: Dziękuje

22 paź 20:24
22 paź 20:33
Saizou :
Potem może się dowiesz albo nie, że zbiór pierwiastków −tego stopnia z jedynki tworzy grupę
22 paź 20:49
Paweł:
Saizou − grupy mieliśmy na kolejnym wykładzie. Przerabiam materiał w kolejności
chronologicznej, więc tym zajmę się za dobrą godzinę.
Mila − bardziej podoba mi się pierwszy sposób, ale dziękuje za drugi. Może kiedyś wykorzystam

Przeglądam materiał, który podlinkowałaś i jednego nie rozumiem.
Napisane jest, że chcąc zaznaczyć Z
4 = { z ∊ C: |z − 4 + 6i| < 2 } na płaszczyźnie
zespolonej liczymy z − z
0 = z − 4 + 6i = z − (4 − 6i) z czego wynika, że z
o = 4 − 6i.
Niby oczywiste.. ale skąd wzięło się z − 4 + 6i? Jeżeli dobrze rozumiem, to standardowo jakbym
chciał zaznaczyć liczbę zespoloną na płaszczyźnie to miałbym np. |z|<2, a tu jest jakby
dorzucona do odległości |z| zespolona 4 − 6i?
22 paź 21:39
Mila:
|z|<2 wnętrze okręgu o środku (0,0).
|z−z0|<2 to jest wnętrze okręgu ośrodku w z0.
Jeżeli środek okręgu to (4,−6) to mamy:
z0=4−6i
|z−(4−6i)|=|z−4+6i| stąd:
|z−4+6i|<2 jest równoważne :
|z−(4−6i)|<2
23 paź 00:07
Paweł: Teraz rozumiem, dziękuje

23 paź 12:18




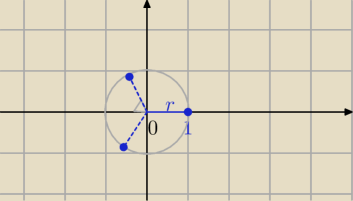 Liczba pod pierwiastkiem to 1.
|1|=1
φ=0
3√1
Liczba pod pierwiastkiem to 1.
|1|=1
φ=0
3√1
 Przeglądam materiał, który podlinkowałaś i jednego nie rozumiem.
Napisane jest, że chcąc zaznaczyć Z4 = { z ∊ C: |z − 4 + 6i| < 2 } na płaszczyźnie
zespolonej liczymy z − z0 = z − 4 + 6i = z − (4 − 6i) z czego wynika, że zo = 4 − 6i.
Niby oczywiste.. ale skąd wzięło się z − 4 + 6i? Jeżeli dobrze rozumiem, to standardowo jakbym
chciał zaznaczyć liczbę zespoloną na płaszczyźnie to miałbym np. |z|<2, a tu jest jakby
dorzucona do odległości |z| zespolona 4 − 6i?
Przeglądam materiał, który podlinkowałaś i jednego nie rozumiem.
Napisane jest, że chcąc zaznaczyć Z4 = { z ∊ C: |z − 4 + 6i| < 2 } na płaszczyźnie
zespolonej liczymy z − z0 = z − 4 + 6i = z − (4 − 6i) z czego wynika, że zo = 4 − 6i.
Niby oczywiste.. ale skąd wzięło się z − 4 + 6i? Jeżeli dobrze rozumiem, to standardowo jakbym
chciał zaznaczyć liczbę zespoloną na płaszczyźnie to miałbym np. |z|<2, a tu jest jakby
dorzucona do odległości |z| zespolona 4 − 6i?
