Suma czwartych potęg koot: Oblicz najmniejszą wartość sumy czwartych potęg pierwiastków równania x²−x+m−2=0 z parametrem m. Z wzorów Viete'a wyliczyłem wzór na sumę czwartych potęg. I doszedłem do tego, że f(m)=2m²−12m+17 , ale nie wiem, co zrobić dalej.

5-latek: Ta funkcja f(m) swoja najmniejsza wartoc ma wierzchoku

koot: No taak, i wierzchołek ma współrzędne (3, −1). Tyle tylko, że m=3 nie należy do wyznaczonej dziedziny (−∞, 9/4), a suma czwartych potęg musi być dodatnia, nie może być równa −1.

5-latek: To w takim razie sprawdz jeszcze raz swoje obliczenia .

===: Zaczynasz od Δ o czym tu nie piszesz. Wierzchołek (jego x_w) nie należy do przedziału wyznaczonego przez Δ Pozostaje Ci więc szukanie wartości najmniejszej ... no właśnie gdzie

koot: Właśnie tego nie wiem, dlatego proszę o pomoc...

===: https://matematykaszkolna.pl/strona/3191.html Pozostaje ci szukanie na krańcach przedziłału

koot: A czy w tym wypadku przedziały nie są otwarte?

Mila:

	9
1)Δ≥0⇔m∊(−∞,		>
	4

	12
mw=		=3
	2*2

	9
3∉(−∞,		>
	4

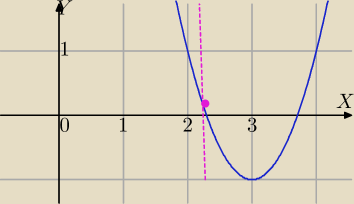
2) f(m)=2m²−12m+17 jest malejąca w przedziale (−∞, 3>

	9
fmin=f(		)
	4

	9		81		9		1
f(		)=2*		−12*		+17=
	4		16		4		8

koot: Dziękuję, Mila

Mila: