Wykres funkcji
Kamil: Dajmy sobie funkcję f(x)
Δ = 4
x1 = 3
x2 = 5
Myślałem że oczywiste jest że wykluczam te liczby z dziedziny i będą tam dwie asymptoty,
ponieważ zerują trójmian kwadratowy, a jednak generator wykresów pokazał zupełnie co innego.
Rozumiem że:
| x2 − 25 | | (x−5)(x+5) | | x+5 | |
| = |
| = |
| |
| x2 −8x + 15 | | (x−3)(x−5) | | x−3 | |
I teraz zgadza się że wykres funkcji w x=5 jest ciągły, ale czy jest jakaś możliwość ustalenia
prawdziwego obrazu funkcji bez jej całkowitego rozkładu i upraszczania?
Zadanie tego typu może być tzw miną, czy istnieje jakaś metoda by od razu to zauważyć?
Dziękuje za pomoc
Pozdrawiam
21 paź 18:23
Janek191:
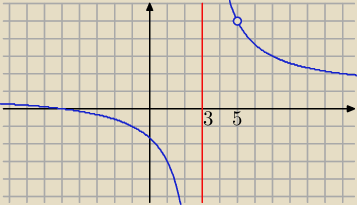
21 paź 18:27
Mila:
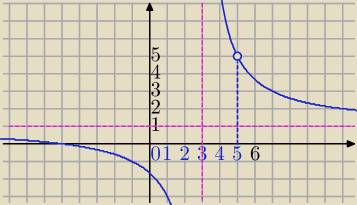
Trzeba rozłożyć na iloczyny licznik i mianownik ( jeżeli to możliwe).
wykres
| | x+5 | |
f(x)= |
| i x≠3 i x≠5 |
| | x−3 | |
| | x−3+8 | | 8 | |
f(x)= |
| =1+ |
| |
| | x−3 | | x−3 | |
21 paź 18:32
5-latek: Kamil
jedyna metoda to rozwiazanie takich kikudziesieciu przykladow .
Wtedy to wszysko zauwazysz . Wedlug mnie nie ma innej . Wiec bierz sie pilnie do pracy jesli
chcesz umiec

21 paź 18:32
Kamil: Rozumiem, trójka pozostaje asymptotą, ale dlaczego 5 wypada z dziedziny skoro wyrażenie
skrócone ma dla sens dla x=5?
21 paź 19:05
Ajtek:
X=5 zeruje mianownik wyjściowego wyrażenia.
Witam Obecnych

.
21 paź 19:10
dsffcd: Wtia
21 paź 19:15

 Trzeba rozłożyć na iloczyny licznik i mianownik ( jeżeli to możliwe).
wykres
Trzeba rozłożyć na iloczyny licznik i mianownik ( jeżeli to możliwe).
wykres

 .
.