Ostrosłup prawidłowy czoworokątny. Far: W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość √6. Kąt dwuścienny między sąsiednimi ścianami bocznymi jest równy 120 stopni. Oblicz: a) odległość spodka wysokości tego ostrosłupa od krawędzi bocznej b) wysokość ostrosłupa

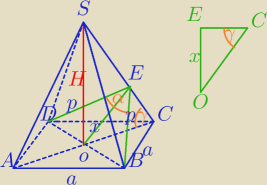
Mila: a=√6 α=120^o BE⊥SC, DE⊥SC OE⊥SC a) |DB|=√6*√2=√12=2√3 W ΔBOE:

	α		|OB|
tg		=		}⇔
	2		|OE

	√3		√3
tg60o=		⇔√3=		⇔
	x		x

|OE|=x=1 b)W ΔBOE: 1) p=2 2) ΔSEO∼ΔSOC⇔

x		|OC|
	=		⇔
H		|SC|

1		√3
	=
H		|SC|

3) W ΔOEC:

	x		1
sinγ=		=		, γ− kąt ostry
	|OC|		√3

sin²γ+cos²γ=1

1		√2		1   3		√6
	+cos2γ=1⇔cosγ=		⇔tgγ=		=
3		√3		√2   √3		6

	H
tgγ=
	|OC|

√6		H
	=		⇔
6		√3

	√2
H=
	2