równanie prostej
czikita: Dane są punkty A = (−1, −2), B = (3, 1), C = (1, 4). Prosta l jest
równoległa do prostej AC i dzieli trójkąt ABC na dwie figury o równych
polach. Znajdź równanie prostej l.
mam równanie prostej ac, pole trojkata i nie wiem co dalej
20 paź 19:13
Kacper: Oblicz długość odcinków na jakie prosta l dzieli pozostałe swa boki trójkąta (np podobieństwo
trójkątów))
20 paź 19:15
===:
... a po co Jej te odcinki

Pytają o równanie prostej ... zna jej współczynnik ... potrzebuje
jeden punkt

20 paź 19:20
czikita: ktoś pomoze to zrobic? w sensie ze policzyc?
20 paź 19:22
===:
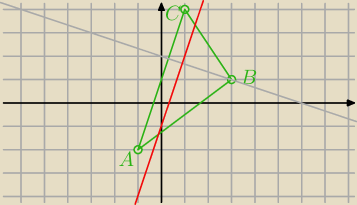
20 paź 19:28
czikita: i jak to dalej liczyc?
20 paź 19:33
===:
podpowiedź: jaka jest skala podobieństwa trójkątów

20 paź 19:45
czikita: 1/2?
20 paź 19:47
Mila:
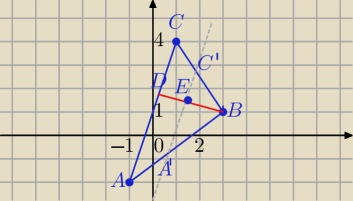
A = (−1, −2), B = (3, 1), C = (1, 4).
AC:
k: y=ax+b
a=3
y=3x+b i C = (1, 4)∊k⇔b=1
k: y=3x+1⇔3x−y+1=0
l: y=3x+b⇔3x−y+b=0
DB⊥AC
A'C' ||AC
ΔC'A'B∼ΔABC
Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa.
Obliczymy DB jako odległość punktu B prostej k
| | |3*3−1+1 | | 9 | |
d(B=(3,1),k)= |
| = |
| |
| | √32+1 | | √10 | |
Teraz
| | |3*3−1+b| | | 9 | |
d(B=(3,1),l)= |
| = |
| |
| | √10 | | √20 | |
Dokończ, posprawdzaj wcześniejsze rachunki.
20 paź 19:52
===:
Odbierasz Jej
Mila przyjemność samodzielnego rozwiązania zadania

20 paź 19:55
Mila:
Przepraszam.

20 paź 20:29
===:
... i żeby to się więcej nie powtarzało ... bo przełożę przez kolano

20 paź 20:34
20 paź 20:49
5-latek: Witam

I moze jeszcze do tego
=== dasz 5 na 4 litery

20 paź 20:50
===:
a gdzieżbym śmiał ... w ogólnie szanowane Ciało Pedagogiczne

20 paź 20:52
czikita: wytlumaczy mi ktos tok rozumowanie Mila?
20 paź 21:07
Mila:
A czego tam nie rozumiesz?
20 paź 21:23
Kacper:
Brakuje wpisania do zeszytu zapewne

20 paź 21:25
czikita: dlaczego EB/DB = 1/√2
20 paź 21:29
Mila:
| | 1 | |
ΔC'A'B∼ΔABC w skali k= |
| |
| | √2 | |
| Wysokość ΔC'A'B | | 1 | |
| = |
| |
| wysokość ΔABC | | √2 | |
20 paź 21:40
czikita: dziekuje

reszte policzylam tylko nie wiem czy dobrze
20 paź 21:48
Mila:
To jaki masz wynik dla b?
20 paź 21:59
Mariusz:
Można spróbować bez podobieństwa
Masz wierzchołki trójkąta więc możesz policzyć równania wszystkich prostych
zawierających boki trójkąta
Szukana prosta jest równoległa do prostej AC więc masz od razu jej współczynnik kierunkowy
Mając dane punkty pole powierzchni możesz policzyć wyznacznikiem
Korzystając z równań prostych BC oraz AB uzależnij rzędne albo odcięte
punktów C' oraz A'
Do wyznacznika dołóż wzór na współczynnik kierunkowy i zobacz co wyjdzie
20 paź 22:18
 Pytają o równanie prostej ... zna jej współczynnik ... potrzebuje
jeden punkt
Pytają o równanie prostej ... zna jej współczynnik ... potrzebuje
jeden punkt 


 A = (−1, −2), B = (3, 1), C = (1, 4).
AC:
k: y=ax+b
a=3
y=3x+b i C = (1, 4)∊k⇔b=1
k: y=3x+1⇔3x−y+1=0
l: y=3x+b⇔3x−y+b=0
DB⊥AC
A'C' ||AC
ΔC'A'B∼ΔABC
A = (−1, −2), B = (3, 1), C = (1, 4).
AC:
k: y=ax+b
a=3
y=3x+b i C = (1, 4)∊k⇔b=1
k: y=3x+1⇔3x−y+1=0
l: y=3x+b⇔3x−y+b=0
DB⊥AC
A'C' ||AC
ΔC'A'B∼ΔABC






 I moze jeszcze do tego === dasz 5 na 4 litery
I moze jeszcze do tego === dasz 5 na 4 litery 


 reszte policzylam tylko nie wiem czy dobrze
reszte policzylam tylko nie wiem czy dobrze