Nierówności logarytmiczne
Natalia: Rozwiąż nierówność
log
3x*log
1/5x<log
1/581
I rozwiązałam to w taki sposób:
| log1/5x | |
| *log1/5x<log1/581 /* log1/53 |
| log1/53 | |
I tutaj jest pytanie skoro mnożę przez liczbę ujemną (bo log
1/53 jest ujemny) to
teoretycznie powinnam zmienić znak,ale wtedy w ostatecznej odpowiedzi mam błąd ze znakami.
| | 1 | | 1 | |
Wychodzi mi że x należy ( |
| ;9), a prawidlowa odpoweidź to x należy (−∞; |
| ) suma |
| | 9 | | 9 | |
(9;
∞). Gdzie jest błąd w moim rozumowaniu
Dalej rozwiązuje to tak:
log
1/5x*log
1/5x>log
1/53
4*log
1/53
t=log
1/5x; t ∊R
t
2>4log
21/53
t
2−4log
21/53>0
(t−2log
1/53)(t+2log
1/53)>0
t∊ (−
∞;−2log
1/53) suma (2log
1/53;
∞)
t<−2log
1/53 lub t>2log
1/53
log
1/5x<−2log
1/53 lub log
1/5x>2log
1/53
Zmieniam znak ze względu na podstawy logarytmu.
Gdzie znajduje się błąd
20 paź 17:21
Jack: Po pierwsze
Log1,53 ≈2,71 wiec jest dodatni a nie ujemny.
20 paź 17:34
Adamm: skąd to zadanie? jak ujemne x mogą być odpowiedzią?
Jack tam jest 1/5 nie 1,5
20 paź 17:40
Jack: Aaa przepraszam zle odczytalem...
Co do postu Adamma.
Faktycznie, jak ujemne x moze byc odpowiedzia skoro zalozenie poczatkowe to x>0
20 paź 17:42
Adamm: źle jest przedział, t∊(−∞;2log1/53)∪(−2log1/53;∞)
20 paź 17:44
Natalia:
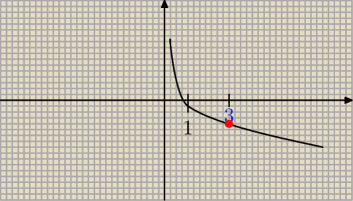
Z wykresu funkcji logarytmicznej:
20 paź 18:17
Natalia: Adamm dlaczego przedział jest źle
20 paź 18:20
Adamm: możesz rozwinąć? twierdzisz że twój przedział jest w porządku?
20 paź 18:21
Adamm: przecież z wykresu widzisz że log1/53 jest ujemny
20 paź 18:23
Natalia:
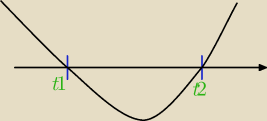
t1= −2log
1/53
t2=2log
1/53
czyli t∊(−
∞;−2log
1/53) suma (2log
1/53;
∞)
20 paź 18:25
Adamm: ok, to czy przedział (2; −1) jest poprawnym przedziałem
według ciebie tak
20 paź 18:26
Natalia: Dobra wiem o co ci chodzi z tymi przedziałami,ale nadal nie wiem co zrobić z zadaniem
20 paź 18:33
Natalia:
20 paź 18:59
Adamm: skoro wiesz o co chodzi z przedziałami to z czym masz problem?
20 paź 19:00
Natalia: Ze znakami. Skoro nie ten przedział to w jakim rozpatruje
t∊(−
∞;−2log
1/53)
20 paź 19:04
Natalia: Czy jednak nie zmieniam znaku przy mnożeniu przez log
1/53
20 paź 19:04
Adamm: no tak, dokładnie to napisałem w poście 17:44
20 paź 19:05
Adamm: jak nie? po prostu przedział jest inny
20 paź 19:05
Adamm: wróć, przedział t∊(−∞;2log1/53)
20 paź 19:06
Adamm: no przecież to nie jest fizyka kwantowa, 2log1/53 jest ujemne, chyba się z tym zgadzasz,
a liczba przeciwna jest dodatnia, i nie ma tu haczyków
20 paź 19:07
Natalia: Czyli:
t<−2log
1/53
20 paź 19:10
Natalia: Dlaczego t∊(−
∞;2log
1/53) skoro z paraboli z 18:25 wynika że albo t∊(−
∞;−2log
1/53) suma
(2log
1/53;
∞) albo t∊(−2log
1/53;2log
1/5)
20 paź 19:12
Adamm: gdyby t należał do tego przedziału, to t∊ℛ ale sprawdź sobie nierówność dla t=0
20 paź 19:15
Natalia: nieprawdziwe, bo −4*coś do kwadratu da nam ujemne
20 paź 19:17
Adamm: no właśnie, dlatego twój przedział, pomimo że jest poprawnie napisany (w sensie formy) to
nie jest niczym uzasadniony, zresztą, na osi x liczby piszemy od najmniejszej do największej
(mówię o twoim poście 18:25)
20 paź 19:20
Adamm: całe to zamieszanie, tylko dlatego że nie potrafisz dojść do wiadomości
że 2log1/53<−2log1/53
20 paź 19:22
Natalia: Ok. Na razie ogarniam. I co dalej
Jak wyznaczyć właściwy przedział który nie będzie kolidował
z innymi twierdzeniami o log
20 paź 19:23
Natalia: Ok. zrozumiałam. zamiast pomyśleć mechanicznie rowziązałam zadanie. BARDZO DZIĘKUJĘ
20 paź 19:24