parametr matthew: Cześć, Mam takie zadanie: wyznacz wszystkie wartości parametru m, dla których funkcja f(x) = (m−1)x² + 2mx − m ma dokladnie 2 m. zerowe jednakowych znaków. Zrobiłem tak: f(x) = (m−1)x² + 2mx − m m−1≠0 m≠1 1^o Δ>0 Δ = (2m)² − 4 * (m−1) * m = 4m² +4m² −4m = 8m² − 4m 8m² − 4m >0 m(8m − 4) >0 m=0 8m−4=0 8m = 4

	1
m =
	2

Nie jestem pewny, czy dobrze zrobiłem....... Bardzo proszę o sprawdzenie... Dziękuję

ula: trochę nie tak {m−1≠0 {Δ>0 {x₁*x₂>0 wzory Vieta pominęłaś ostatni warunek i policzyłaś źle Δ Δ=(2m)²−4(m−1)*m>0 4m>0 m>0

jo: Ponieważ miejsca zerowe mają być jednakowych znaków to jeszcze trzeba skorzystać ze wzorów Viete'a.

ula: x₁*x₂=^c_a

−m
	>0
m−1

m*(m−1)<0 0 1 m∊(0;1) część wspólna wszystkich zalożeń m∊(0;1)

ula: jeszcze raz przeliczyłam Δ ty masz dobrze zgubiłam − x∊(−∞;0)suma(¹₂;∞) m∊(0;1) → m∊(¹₂;1)

dede: Poprawne warunki zad. to: 1/ m≠1 i 2/ Δ≥0 ( bo mogą być dwa takie same ( bo tych samych znaków) i 3/ x₁*x₂ >0 poprawna odp : m€ < ¹₂, 0)

matthew: a dlaczego, musze jeszcze skorzystać ze wzorów Viete`a? Czyli tak... bo juz pogubiłem ... co mam dobrze, pierwsze dwa warunki, tak? trzecim warunkiem są wzory Viete`a?

sssss: 1 warunek : jest po to aby byla to funkcja kwadratowa 2 warunek : Δ>0 aby mial DOKLADNIE 2 miejsca zerowe (to do dede) 3 warunek : Wzor Viete'a , aby oba miejsca zerowe byly tych samych znakow.

dede: bo x₁*x₂ = ( −)*(−) >0 i x₁*x₂ = ( +)*(+) >0 czyli jak obydwa jednakowych znaków , to ich iloczyn >0 zatem 3/ warunek: ^c_a >0

dede: Niech Anna to potwierdzi że Δ≥0 ...... to może wreszcie uwierzycie

sssss: Jezeli obydwa sa takie same , czyli x₁= 1 i x₂ = 1 , to jest 1 miejsce zerowe.

matthew: Czyli cos takiego?

	c
x1 * x2 =
	a

2m
	> 0 /* (m−1)2
m−1

2m(m−1) > 0 2m² −2m >0 m(2m−2) > 0 m=0 2m−2=0 2m = 2 m = 1

matthew: x₁ + x₂ >0

	−b
x1 + x2 =
	a

−2m
	>0 /* (m−1)
m−1

−2m(m−1) > 0 −2m² + 2m >0 −2m(m−1)>0 m=0 m=1

dede: dosssss jakie jedno x₁=1 v x₂= 1 −−− to jedno podwójne ( czyli dwa takie same ) gdyby było napisane dwa różne miejsca zerowe to wówczas Δ >0 więcej nie dyskutuję , bo to dla mnie banał

sssss: Matthew, zle wstawiles. x₁ * x₂ = ^c_a ^−m_m−1 > 0 −m(m−1)>0 m=0 ∨ m=1 m∊(0,1) czesc wspolna wszystkich : ( 0 ; ¹₂ ).

sssss: do dede: Postepujac wedlug Twojej teorii , ze mozna miec 2 takie same miejsca zerowe, to rowniez mozna miec 10000000000000000 miejsc zerowych, o takiej samej wartosci. x₁ = 1 , x₂ = 1 , x₃ = 1 , x₄= 1 .... x₉9999999999999 = 1 . Einstein!

dede: równanie kwadratowe nie może mieć więcej niż dwa miejsca zerowe więc nie może mieć ich 1000

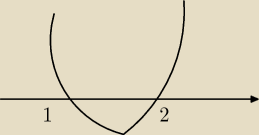
sssss: Wiem , ale tak czy inaczej , jak komus udowodnisz ze rownanie ma 2 takie same pierwiastki? rysunek przedstawia 2 miejsca zerowe

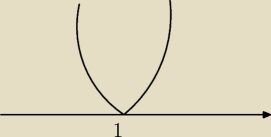
sssss: a tak ma 1

sssss: dede: czyli w takim razie, jesli robiac zadanie, wyjdzie mi Δ=0 , to czy mam napisac x₁=1, x₂=1 ?

sssss: dede: wstaw 1/2 , ktora wedlug Ciebie zalicza sie do rozwiazania, pod m. po wstawieniu , Δ=0 , co daje nam jedno rozwiazanie, niezgodne z trescia zadania. Pozdrawiam

dede: piszesz x₁=x₂= 1 ale w zad. z parametrami juz bierzemy pod uwagę jaka jest treść zadania; gdyby było ma dwa różne pierwiastki ; to Δ>0 " " " " pierwiastki różnych znaków ; to Δ>0 " " dwa pierwiastki ujemne : to Δ≥0 " " " " " dodatnie : to Δ≥0 " " " dwa pierwiastki : to Δ≥0 itd. itp.

Bogdan: Potwierdzam słowa dede. Witaj Eto

sssss: No coz, w takim razie przegralem te bitwe jeszcze sie zapytam moich nauczycieli , bo do konca nie jestem przekonany.

Eta: Witaj Bogdanie