wysokość ostrosłupa
ja : W kulę o promieniu 2 cm wpisano ostrosłup prawidłowy czworokątny o objętości
163 cm
3.
Oblicz wysokość tego ostrosłupa.
wiem że było już takie zadanie (
https://matematykaszkolna.pl/forum/319704.html) jednak robiąc je i tak źle mi wyszło : ( Może ktoś
pomoże ?
18 paź 22:37
Mila:
Jaka jest odpowiedź?
18 paź 23:23
piotr: h − wysokość ostrosłupa
p− przekątna tego ostrosłupa.
16/3=h*p2/6
(2−h)2 + p2/4 = 4
⇒h=2, p=4
lub
h=1+√5, p=2 √2√5−1)
18 paź 23:23
piotr: p− przekątna podstawy ostrosłupa.
18 paź 23:23
piotr: h=1+√5, p=2 √2(√5−1)
18 paź 23:27
Mila:
H∊(0,4)
18 paź 23:41
Mila:
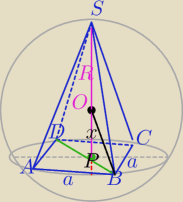
|OP|=x
a2*H=16
I) przypadek : podstawa ostrosłupa leży poniżej środka kuli
H>R
H=x+R⇔H=x+2, x>0, x<2 lub (II) H<R⇔ H=R−x ( zrobię drugi rysunek)
a
2*(x+2)=16
Promień okręgu opisanego na ΔDBS i ΔACS jest równy promieniowi kuli.
|DB|=a
√2
W ΔOPB:
2x
2+a
2=8
a
2=8−2x
2
Podstawiamy do równania: a
2*(x+2)=16
(8−2x
2)*(x+2)=16
8x+16−2x
3−4x
2=16
−2x
3−4x
2+8x=0
−2x* (x
2+2x−4)=0
x=0 lub x=U{
√5−1}
H=R=2
lub
H=√5+1
==========
II
H=2−(
√5−1)=3−
√5
==============
18 paź 23:43
ja : w odpowiedziach jest że h =8 lub h = 1+ √17
19 paź 07:56
piotr1973: h może być w granicach od 0 do 2r=4, h =8 lub h = 1+ √17 nie należą do tego przedziału
19 paź 08:29
ja : uuu no to nie mam pojęcia co jest źle XD
19 paź 15:00
Mila:
Sprawdź treść.
19 paź 17:12
ja : treść dobrze
20 paź 14:01
5-latek: Skoro tresc jest ok to wstaw screma tutaj z tym zadaniem
20 paź 14:35
Mila:
Z jakiej książki to zadanie?
20 paź 17:06
 |OP|=x
|OP|=x