Proszę o sprawdzenie prostego zadania xyz: Mam daną nierówność: ^x2+x−2_x+3≤0 Dziedzina: x+3≠0 x≠−3 D x∊R {−3} (x²+x−2)(x+3)≤0 Δ=9 pierwiastek z delty=3 x₁=−2 x₂=1 I teraz pytanie, czy −3 też jest miejscem zerowym funkcji? Mam wynik x∊<−2,1>, ale nie jestem pewny czy −3 to miejsce zerowe, bo jeśli tak to kolejnym rozwiązaniem byłoby x∊<−∞,−3>

Adamm: dla nieskończoności zawsze przedział otwarty narysuj sobie normalnie jakbyś rozwiązywał nierówność wielomianową i od odpowiedzi odejmij tylko 3, nie cały przedział

xyz: Mam narysowany wykres, tylko nie wiem czy −3 jest miejscem zerowym czy nie.

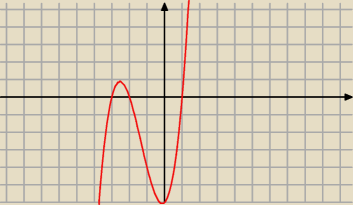
Adamm: (x−1)(x+2)(x+3)≤0 ⇔ x∊(−∞;−3>u<−2;1> z uwzględnieniem dziedziny x∊(−∞;−3)u<−2;1>

PW: Jak może być miejscem zerowym, skoro nie należy do dziedziny? Warto dziedzinę powtarzać na każdym etapie, np. pisać (x² −+ x − 2)(x + 3) ≤ 0, x ≠ −3. Na "wężu" rysujesz "puste kółko".

5-latek: A gdzie tutaj jest funkcja ?