Narysuj następujące zbiory VRally: Dzień dobry, Mam następujące zadanie. Wstawię tylko 2 przykłady. Narysować zbiory (a) {(x, y) ∈ R²: x + y > 2 ∨ x < 3}, (b) {(x, y) ∈ R²: x > y =⇒ (2x < y =⇒ x² + y² = 3)}, (c) {x ∈ R : ∃y ∈ R : x² + y² ≤ 1}, Niekoniecznie proszę o zrobienie ale o klarowne wytłumaczenie

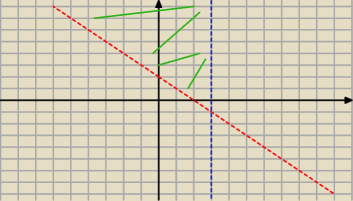
Adamm: (a) y>2−x, szukamy wartości nad prostą oraz x<3

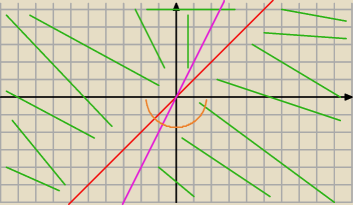
Adamm: jeśli x>y to z 2x<y musi wynikać x²+y²=3 f. czerwona to y=x różowa to y=2x z tego wynika że jeśli x≥y to równanie zachodzi, jeśli y≥x oraz 2x≥y równanie również zachodzi jedyny obszar którego zbiór nie posiada to 2x≤y≤x za wyjątkiem części okręgu

VRally: Dziękuję Co dokładnie oznacza R²? Rzeczywiste do kwadratu? Jak to interpretować?

Adamm: 2x≤y≤x powinno być 2x<y<x

Adamm: płaszczyzna

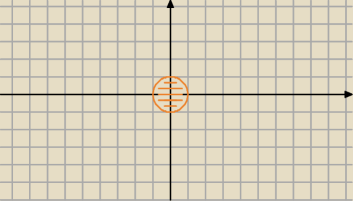
Adamm: zwykłe równanie koła

VRally: Jeszcze mam taki przykład − podobny do (b) {(x, y) ∈ R²: x² + y² = 1 =⇒ 2x = y} I to samo pytanie zarówno do tego przykładu jak i przykładu (b). Jak odwołać się do x² + y² = 1? Czy jest to równanie koła o środku w punkcie (0,0)?

Adamm: tak, o promieniu r=√1=1 wszystkie współrzędne należą, zmiana zachodzi jedynie dla koła, jeśli punkt leży na kole to musi leżeć na 2x=y

VRally: Super, już wszystko rozumiem. Dziękuję za pomoc