Podaj dziedzinę funkcji f i naszkicuj jej wykres. cotyniepowiesz98: f(x)=log₂ (|x| + 4)

Janek191: I x I + 4 > 0 ⇒ D = ℛ

cotyniepowiesz98: Dziedzina wychodzi mi, że to liczby rzeczywiste, jednak nie zgadza mi się z wykresem, gdyż na −4 pojawia się asymptota. (Najpierw przesunięcie o 4 w lewo, następnie to co jest po prawej stronie układu odbijam na lewą?)

cotyniepowiesz98: |x| >−4 , x należy do R, bez wątpienia...

cotyniepowiesz98: Z wykresu wychodzi, że niby ta asymptota, ale jakby podstawić −4 za x, to otrzymujemy log₂ 8, czyli wartość jest równa 3.

cotyniepowiesz98: Więc może po przesunięciu ta asymptota po prostu traci swoją ważność...? Nie mam pojęcia

cotyniepowiesz98: Dzięki bardzo

piotr1973: funkcja jest parzysta, więc narysuj dla x≥0 i potem lustrzane odbicie względem OY

cotyniepowiesz98: funkcja jest parzysta, więc narysuj dla x≥0 i potem lustrzane odbicie względem OY Jestem w liceum i korzystam jednak z zalozen, które są w karcie wzorow, jednak dziekuje bardzo Dla pewności zadam jeszcze raz pytanie: x należy do R, przeżywam podstawowy wykres y=log₂ o 4 w lewo, następnie mając w nosie asymototę , rysuje odbicie tego co jest po prawej, na lewą stronę?

cotyniepowiesz98: Przesuwam *

cotyniepowiesz98: Mam jeszcze do tego podać wzór funkcji y=g(m) opisującej liczbę rozwiązań równania f(x)=m w zależności od parametru m. Także : 0 rozwiązań dla m należącego (− nieskończoność, 2) 1 rozwiązanie dla m =2 2 rozwiązania dla m należącego (2,nieskonczonosc)

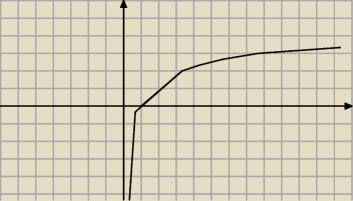
5-latek: Powiedzmy ze to jest wykres y=log₂x Pokaz mi jego asymtote

cotyniepowiesz98: Asymptota y=log₂ lezy na x =O, a funckji z zadania na x=−4

5-latek: To oznacza ze byly granice i pochodne Wiec po co pytasz o to jak rysowac tak prosty wykres ?

5-latek:

cotyniepowiesz98: Dzięki Jerzy

cotyniepowiesz98: Jeśli znajdziesz chwilę to mógłbyś zetknąć na drugą część zadania (tę z parametrem)? Z góry wielkie dzięki!

Omikron: Cotyniepowiesz98, przy przekształceniu y=f(|x|) wszystko znajdujące się na lewo od osi Oy znika i zostaje zastąpione przez odbicie prawej strony. Asymptota w tym przykładzie jest po lewej stronie więc znika.