Fee Alek: Jak sprawdzić czy podpunkt c jest prawdziwy zdj http://imgur.com/jels7ZU

Janek191:

	1
p1 : y =		x2 −2 x + 3
	2

	1
p2 : y =		x2 + 4 x + 5
	2

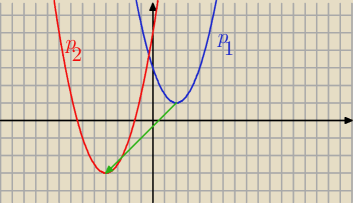
Odp.Parabola p₂ powstaje po przesunięciu p₁ o wektor [ − 6, − 4] c) Nie zachodzi, bo √(−6)² + (−4)² = 2√13 ale też √ 6² + ( − 4)² = 2√13

Janek191: ?

Janek191: Czy zrozumiałeś rozwiązanie ?

Janek191: A to, że parabola p₂ powstaje z p₁ w wyniku translacji o q wektor [ − 6, − 4] ?

Janek191: q zbędne

Janek191: P = ( x, y) → w = [ a , b] to P' = ( x + a, y + b) zatem x ' = x − 6 ⇒ x = x' + 6 y ' = y − 4 ⇒ y = y ' + 4 Wstawiam za x i za y do równania paraboli p₁: y ' + 4 = 0,5*( x ' + 6)² − 2*(x'+ 6) + 3 y ' + 4 = 0,5*( x'² + 12 x ' + 36) −2 x' − 12 + 3 y ' + 4 = 0,5 x'² + 6 x' + 18 + −2 x ' − 9 y ' = 0,5 x'² + 4 x' + 5 Opuszczam primy i otrzymuję równanie parabolo p₂ y = 0,5 x² + 4 x + 5 ===============

Alek: tak rozumiem już bardzo fajnie wytłumaczone

Janek191: c) Nie, bo wektorów o długości 2√13 jest nieskończenie wiele. Między innymi wektory [ − 6, − 4] ale i [ 6, − 4] , [ 6, 4] , [ − 6, 4] różne od [ − 6, − 4] ale o tej samej długości.