Ciagi Rafalori: Witam. 5 lat bez matematyki jestem dlatego mam pytanie jak to rozwiazac an= 1− 1/n an= 1/ 2 do potęgi n an= 1− 1/2 do potęgi 2 Rzecz jasna mowa o ciagach.

Jerzy: Rzecz jasna musi być jakieś polecenie w zadaniu.

piotr1973: a jakie jest polecenie?

PW: No …"jak to rozwiązać".

5-latek: Pewnie studia a tu zonk

Janek191: Obliczyć granice tych ciągów ?

Janek191:

	1
an = 1 −
	n

więc

	1
lim an = lim 1 − lim		= 1 − 0 = 1
	n

n→∞ n→∞ n→∞

Janek191:

	1
an =
	2n

lim a_n = 0 n→∞ bo lim 2ⁿ = +∞ n→∞

5-latek: Witam A Ty Janek191 jak zwykle musisz sie domyslac jesli sie jeszce nie domysliles to przez takie cos wlasnie to forum traci na znaczeniu bo byle lajza tu wpiszse co popadnie i dostanie rozwiaznie (bo zawsz sie ktos domysli co autor mial na mysli Przepraszam jesi Cie urazilem .

Rafalori: Może chodzi tu o monotonicznosc? Dokladnie STUDIA

Jerzy: To wstyd student ,żeby nawet nie przepisać treści zadania !

Rafalori: Hoho. Jerzy nie bądź bardziej irytujący niż jesteś.

Janek191:

	1
an = 1 −
	n

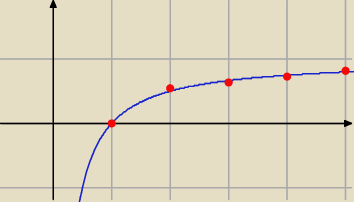
Ten ciąg jest rosnący, bo a_n+1 − a_n > 0 Patrz też na wykres

5-latek: I tak oto to forum UPADA Janek 191 mialem bardzo duzy szacunek dla Ciebie (ze wzgledu na wiek i wiedze jednak teraz .....

Mariusz: Rafał podaj zwartą postać funkcji tworzącej dla tych ciągów (takiej funkcji tworzącej która dla ciągu jedynek daje sumę szeregu geometrycznego dość często jest jeszcze używana taka funkcja tworząca która dla ciągu jedynek daje exponentę)

	1
an=1−		tutaj dla n=0 będzie problem (dzielenie przez zero)
	n

chyba że zera nie zaliczacie do liczb naturalnych (u mnie zaliczali)

faust: zdarzenia A i B są niezależne. Udowodnij, że zdarzenia A∪B i C też są niezależne.

jc: Przyłączę się do 5−latka. Systematycznie pojawiają się polecenia: rozwiąż ciąg, całkę, szereg, oblicz styczną, zbieżność, równanie, itp. Często brakuje nawiasów. I co z tego, że uczeń lub student zobaczą rozwiązanie? Potem się dziwi, dlaczego nie ma zaliczenia, choć coś tam napisał, czasem nawet w części dobrze. A w rozmowie takie braki od razu wychodzą. Dlatego oczekujmy, że choć treść zostanie w miarę sensownie zapisana. W powyższym zadaniu mogły być inne pytania: czy ciąg jest monotoniczny, czy jest ograniczony, jak wygląda zbiór wartości, itp.