zadanie z dawnej matury Rafał: W prosty ścięty stożek wpisano kulę o promieniu r=2 cm, której objętość ma się do objętości stożka jak 8:21. Oblicz promienie obu podstaw stożka. Wystarczy mi sama odpowiedź. W moich super długich rachunkach mam bałagan i od godziny szukam błędu.

Antonni: A mozesz napisac z jakiego zbioru jest to zadanie ?

Rafał: http://wiadomosci.gazeta.pl/wiadomosci/56,114944,17862788,zabor-austriacki-pytania-maturalne-z-krakowskiego-liceum-sw,,2.html

Eta: a=4 −−− dł. promienia dolnej podstawy stożka b= 1 −−−dł. " " górnej podstawy stożka

Mila: r=1 R=4

Mila: Witaj Eto.

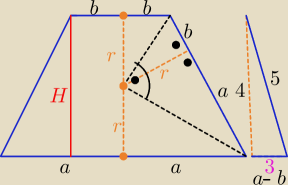
Eta: a −− dł. promienia podstawy dolnej b −−− dł. " " " górnej H=2r= 4 , r²=a*b ⇒ ab= 4

	4		32π		πH
Vk=		πr3 =		i Vst śc.=		(a2+ab+b2)
	3		3		3

to

8		8
	=		⇒ a2+b2= 17 ⇒ (a+b)2−2ab=17 ⇒ a+b=5
21		a2+ab+b2

Z trójkąta prostokątnego ( mały obok) a−b=3 to a+b= 5 i a−b=3 −−−−−−−−−− 2a=8 ⇒ a=4 to b= 3 ===============

Eta: Witaj Mila

Eta: Poprawiam zapis : oczywiście,że a=4 i b= 1

Eta: I co na to ...... Rafał ?

Rafał: Znalazłem u siebie błąd, za chwilę przeanalizuję rozwiązanie, bo wygląda o wiele prościej od mojego

Mila: Ja wykorzystałam równanie wynikające z ilorazu objętości, z własności okręgu wpisanego w czworokąt ( sumy przeciwległych boków równe), tw. Pitagorasa. Trochę więcej liczenia, ale wyniki mamy zgodne.

Eta:

Rafał: To ja chyba wybrałem najgorszą drogę z możliwych W każdym razie, dziękuję wszystkim za pomoc

Mila: No i co to za mina Rafale, rozwiąż jeszcze raz wszystkimi sposobami, porównaj i wnioski. Ważne, że rozwiązałeś.

Jack: Ktoś tu wrócił do pierwotnej nazwy Ja natomiast muszę się nauczyć całego alfabetu greckiego, gdyż "bez tego ani rusz" (jakbym nie miał co robić...eh)

Eta: