Okrąg wpisany w trójkąt, pomocy :(
Iggy: W trójkąt równoramienny o kącie przy podstawie równym 30 st. wpisano okrąg o promieniu 3.
Oblicz długości boków trójkąta
16 paź 16:21
Mila:
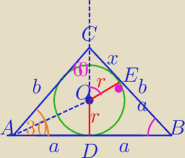
|AB|=2a
|CD|=h
|EB|=a
ΔCEO∼ΔCDB
| | CE | | √3 | | |CE| | |
W ΔCEO: tg30= |
| ⇔ |
| = |
| ⇔ |
| | r | | 3 | | 3 | |
|CE|=
√3
=======
b=a+√3
| | a | | √3 | | a | |
W ΔCDB: sin60= |
| ⇔ |
| = |
| |
| | b | | 2 | | a+√3 | |
2a=
√3*(a+
√3)
2a=
√3*a+3
2a−
√3a=3
a*(2−
√3)=3 /*(2+
√3)
a*(4−3)=3*(2+
√3)
a=3*(2+
√3)
b=6+3
√3+
√3
b=6+4
√3
|AB|=2a=6*(2+
√3)
|AC|=|BC|=6+4
√3
===========
16 paź 17:42
Eta:
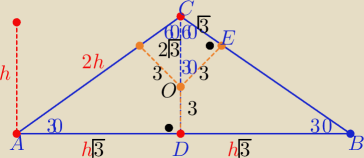
Można z trójkątów "ekierek" o kątach 30
o,60
o , 90
o
które ułatwiają rozwiązanie:
h= 2
√3+3
|AC|=|BC|= 2h= 2(2
√3+3)
|AB|= 2h
√3= 6(
√3+2)
16 paź 18:37
 |AB|=2a
|CD|=h
|EB|=a
ΔCEO∼ΔCDB
|AB|=2a
|CD|=h
|EB|=a
ΔCEO∼ΔCDB
 Można z trójkątów "ekierek" o kątach 30o,60o , 90o
które ułatwiają rozwiązanie:
h= 2√3+3
|AC|=|BC|= 2h= 2(2√3+3)
|AB|= 2h√3= 6(√3+2)
Można z trójkątów "ekierek" o kątach 30o,60o , 90o
które ułatwiają rozwiązanie:
h= 2√3+3
|AC|=|BC|= 2h= 2(2√3+3)
|AB|= 2h√3= 6(√3+2)