Geometria analityczna - styczna do okręgu
Ilona: hej

mam problem z takim zadaniem:
Oblicz tangens kąta ostrego, jaki tworzą styczne do okręgu o: x
2+y
2−8x−6y+21=0, przechodzące
przez punkt P(2, −1).
Obliczyłam równanie okręgu: (x−4)
2+(y−3)
2=4 − więc mam S i r. W sumie nie wiem co dalej

haczyk jest taki, że jedyny rysunek jaki mogę wykonać to pomocniczy, czyli bez danych. Czy
ktoś mi pomoże?
Z góry dziękuję za odpowiedź

16 paź 14:26
Janek191:
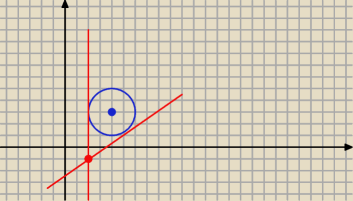
16 paź 14:38
Ilona: wiem, że jedna z stycznych, to x=2 lecz jeśli wykonujesz sobie zwykły rysunek pomocniczy, bez
układu współrzędnych, to raczej Ci to nie wyniknie. Chodzi o to, aby wszystko obliczyć, a nie
odczytać.

16 paź 14:41
Adamm: y=ax+b
równanie ma spełniać równanie okręgu oraz przechodzić przez punkt
−1=2a+b
b=−1−2a
y=ax−1−2a
(x−4)2+(y−3)2=4
(x−4)2+(ax−1−2a−3)2=4
(a2+1)x2−(4a2+8a+8)x+4a2+16a+28=0
szukaj takiego a że Δ=0
16 paź 14:46
Ilona: super! dziękuję bardzo

16 paź 14:54
Janek191:
→
PS = [2, 4 ]
→
PK = [ 0, 3 ]
| | 12 | | 4 | | 2 | |
cos β = |
| = |
| = |
| |
| | √20*3 | | 2√5 | | √5 | |
| | 2 tg β | | 1 | | 4 | |
tg α = tg 2β = |
| = |
| = |
| |
| | 1 − tg2 β | | 1 − 14 | | 3 | |
16 paź 15:00
Janek191:
Pomyłka
→
PK = [ 0, 4]
16 paź 15:02
Ilona: Janek191 − skąd wziąłeś punkt K? Co to za punkt?
16 paź 15:05
Janek191:
Wszystko źle − coś mi się pokićkało

16 paź 15:07
Janek191:
K − punkt styczności prostej stycznej pionowej
K = (2, 3)
16 paź 15:08
Ilona: świetny sposób

dziękuję.
16 paź 15:11
Janek191:
→
PS = [ 2, 4]
→
PK = [ 0, 4]
→ →
β = I ∡ ( PS , PK) I
| | 2*0 + 4*4 | | 4 | | 2 | |
cos β = |
| = |
| = |
| |
| | √20 * 4 | | 2√5 | | √5 | |
itd.
Jednak jest dobrze

16 paź 15:15
 mam problem z takim zadaniem:
Oblicz tangens kąta ostrego, jaki tworzą styczne do okręgu o: x2+y2−8x−6y+21=0, przechodzące
przez punkt P(2, −1).
Obliczyłam równanie okręgu: (x−4)2+(y−3)2=4 − więc mam S i r. W sumie nie wiem co dalej
mam problem z takim zadaniem:
Oblicz tangens kąta ostrego, jaki tworzą styczne do okręgu o: x2+y2−8x−6y+21=0, przechodzące
przez punkt P(2, −1).
Obliczyłam równanie okręgu: (x−4)2+(y−3)2=4 − więc mam S i r. W sumie nie wiem co dalej haczyk jest taki, że jedyny rysunek jaki mogę wykonać to pomocniczy, czyli bez danych. Czy
ktoś mi pomoże?
Z góry dziękuję za odpowiedź
haczyk jest taki, że jedyny rysunek jaki mogę wykonać to pomocniczy, czyli bez danych. Czy
ktoś mi pomoże?
Z góry dziękuję za odpowiedź 




 dziękuję.
dziękuję.
