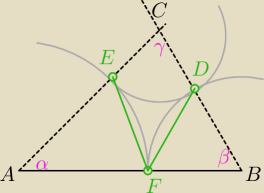
Udowodnij, że ∡EFD = U{α + β}{2} = 90• - U{γ}{2} Ola: Dany jest trójkąt ABC, w którym ∡BAC = α, ∡ABC = β oraz ∡ACB = γ. Na bokach BC, AC i AB tego trójkąta wybrano odpowiednio punkty D, E i F w taki sposób, by AE = AF, BD = BF, CD = CE.

	α + β		γ
Udowodnij, że ∡EFD =		= 90• −
	2		2

	γ
Ogólnie mam problem jak udowodnić, że ten kąt to 90• −
	2

===: było niedawno ... poszukaj

Ola: Właśnie szukałam, ale znalazłam tylko rozwiązanie na innej stronie, które w dodatku nie było dokończone Dlatego jeśli mogę prosić byłabym wdzięczna za pomoc w znalezieniu, albo chociaż

	γ
wytłumaczenie, czemu to jest 90• −
	2

Tadeusz:

	α+β
skoro już wiesz dlaczego ∡EFD=		a α+β=180−γ to czego nie rozumiesz?
	2

Tadeusz:

	180o−α		180o−β		α+β
∡EFD=∡AFE−∡BFD=180o−		−		=
	2		2		2

Tadeusz: oczywiście miało być ∡EFD=180−∡AFE−∡BFD