trapez Michał: W trapezie ABCD (AB∥CD) dwusieczna kąta wewnętrznego BAD jest prostopadła do ramienia BC i dzieli go w stosunku 2:1 licząc od wierzchołka B. Wyznacz stosunek pól figur na jakie ta dwusieczna podzieliła trapez. Pomoże mi ktoś? Rysunek mam zrobiony ale sam nic nie mogę wymyślić Wiem że jst późna pora i nie musi być teraz bo mam to zadane na poniedziałek

wmboczek: przedłużamy ramiona trapezu i otrzymujemy trójkąt oznaczamy kąty przy podstawie α i 90−α i okazuje się, że mamy równoramienny z wysokością będącą dwusieczną z podobieństwa wyznaczymy zależność między podstawami trapezu a=4b Ptrapezu=2,5bh Pdolnej=2/3*1/2*4b*h=4/3bh Pgórnej=(5/2−4/3)bh ....

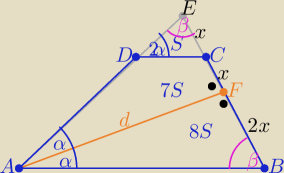
Eta: To może tak: Dwusieczna d ⊥BC ⇒ ( po przedłużeniu ramion)ΔABE równoramienny z podobieństwa trójkątów ABE i DCE z cechy (kkk)

	4x
skala k=		= 4
	x

oznaczam P(DCE)=S to P(ABE)=k²*S= 16S i P(ABF)= 8S i P(AFCD)= 8S−S= 7S

P(AFCD)		7S		7
	=		=
P(ABF)		8S		8

=======