Funkcje trygonometryczne muka: Prosiłbym o rozwiązanie zadania: sinx−√3cosx >1 Po zamianie doszedłem do tej postaci:

	π		1
sin(		− x) >
	3		2

Ajtek:

	1		π
Zauważ, że sinx=		zatem sinx=sin		, czyli:
	2		6

	π		π
sin(		−x)>sin
	3		6

Dalej dasz sobie radę.

muka: Właśnie troszkę mój wynik się nie zgadza z tym co mam w odpowiedziach, inaczej bym tutaj nie pisał.

Ajtek: Przekształceń nie sprawdzałem, masz pole do popisu. Znajdziesz ewentualny błąd, będziesz wielki. Pokaż odpowiedź i rozwiązanie, finalne. Może to jest tożsamość.

muka:

	π		2
Powinno wyjść		+2kπ < x <		π +2kπ
	2		3

	π
Mi wychodzi x<		.
	6

muka:

	π		7
Przepraszam, za błąd		+2kπ < x<		π +2kπ
	2		6

Ajtek: No to i mój błąd, Funkcja sinx ma okres 2π

muka: Powiem szczerze, że nie bardzo pamiętam i przez to nie rozumiem co to zmienia.

muka: Już sobie przypomniałem. Dziękuję za podpowiedź !

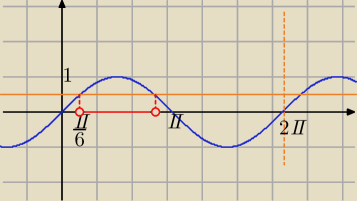
Mila: sinx−√3cosx >1 /:2

1		√3		1
	sinx−		cosx>
2		2		2

	π		π		1
sinx*cos		−sin		*cosx>		⇔
	3		3		2

	π		1
sin(x−		)>
	3		2

π		π		5π		π
	+2kπ<(x−		)<		+2kπ /+
6		3		6		3

π		7π		π
	+2kπ<x<		+2kπ /+
2		6		3