Wyznacz liczbę rozwiązań równania w zależności od wartości parametru m. Kasia: Wyznacz liczbę rozwiązań równania w zależności od wartości parametru m. W przypadku istnienia rozwiązań wyznacz je. |x+2|−|x−1|=m otóż wyznaczam liczbę rozwiązań: dla m∊(−∞,−3) brak rozwiązań dla m=−3 równanie ma nieskończenie wiele rozwiązań: x∊(−∞,−2) dla m ∊(−3,3) równanie ma 1 rozwiązanie: x∊<−2,1> dla m=3, równanie ma nieskończenie wiele rozwiązań x∊(1,∞) dla m∊(3,∞) równanie nie ma rozwiązania Czy jest to poprawne rozwiązanie, ponieważ w odpowiedziach wychodzą inne przedziały: dla m=−3; x∊(−∞,−2> dla m=3: x∊<1,∞) dla m∊(−3,3) jedno rozwiązanie x=^m−1₂ proszę o odpowiedź

PW: Skąd atak na m = −3? − ono niczemu nie jest winne. Na pewno podałaś właściwe zadanie?

Kasia: tak, zadanie jest poprawne

PW: Rozumiem, że pominęłaś rozważania o przedziałach i podajesz końcowe wnioski, ale jest to niezrozumiałe. Na przykład dla x > 1 mamy do czynienia z równaniem x + 2 − (x − 1) = m, x∊(1,∞) 3 = m, x∊(1,∞). Tu wniosek jest poprawny, dla m = 3 wszystkie x z podanego przedziału są rozwiązaniami. Dla x < − 2 równanie ma postać − x − 2 − (−x + 1) = m, x∊(−∞, −2) − 3 = m, x∊(−∞, −2) − tu też wniosek poprawny. Napisz spokojnie: − dla x ∊ <−2, 1> równanie ma postać:

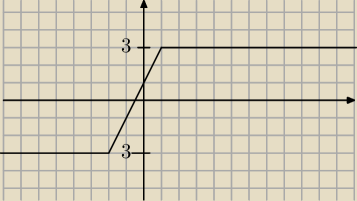
5-latek : To jest wykres funkcji f(x)= |x+2|−|x−1|