Okręg opisany na trójkącie Iggy: Wyznacz promień okręgu opisanego na trójkącie równoramiennym: a) o ramieniu b i kącie alfa przy podstawie b) o wysokości h opuszczonej na podstawę oraz kącie 2alfa między ramionami

myszka:

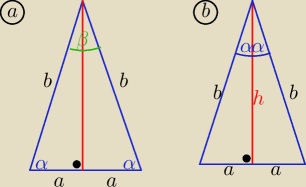
	2P
a) P=rp r=		i β=180o−2α sinβ= sin(2α)
	2a+2b

2P= b²*sinβ= b²*sin2α a=b*cosα to 2a+2b=2b(cosα+1)

	b2sin(2α)		2bsinαcosα		bsinαcosα
r=		⇒ r=		=
	2b(1+cosα)		2(1+cosα)		1+cosα

b) podobnie.......

	hsinα		h
2P=a*h a=h*tgα=		i b=
	cosα		cosα

	2h(1+sinα)
to L= 2a+2b=
	cosα

	2P
r=		= ............ dokończ
	2a+2b