Trygonometria - trapez miki992: Długości podstaw trapezu są równe 5 i 20 a jego przekątne przecinają się pod kątem prostym. Oblicz cosinusy kątów nachylenia przekątnych do dłuższej podstawy, jeśli wysokość trapezu jest równa 12.

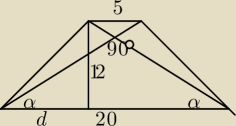
Adamm: trapez ten jest równoramienny

	20−5
d=		=7,5
	2

	20−d
cosα=
	√122+(20−d)2

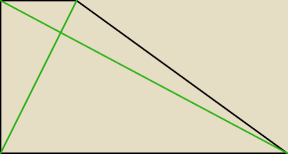
ax: a może taki?

myszka:

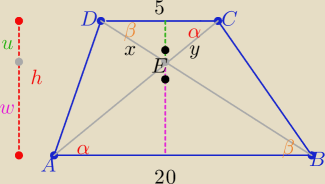
	20
Z podobieństwa trójkątów ABE i DCE skala k=		=4
	5

	1		12
to u=		*h =
	5		5

	x*y		12   *5 5
w ΔDEC : P(DEC)=		=		⇒ xy=12
	2		2

oraz x²+y²=25 ⇒ (x+y)²−2xy=25 ⇒ (x+y)²=49 to x+y= 7 i xy=12 ⇒ x=3 i y=4 lub x=4 i y=3

	3		4		4		3
zatem: cosβ=		i cosα=		lub cosβ=		i cosα=
	5		5		5		5

=======================================

myszka: @Adamm

	√2
gdyby trapez był równoramienny to kąty α=β= 45o ⇒cosα=cosβ=
	2

ale wtedy wysokość h =12,5 ≠12