Liczby Zespolone Dyb: Liczby zespolone Oblicz pierwiastki równania: w³−i=0 w=³√i, w=−³√i, w=i dobrze zrobiłem?

ICSP: źle. w³ +i³ = 0 (w + i)(w² − wi − 1) = 0 drugie równanie jest równaniem kwadratowym.

Dyb: ale tam nie było w³+i³=0 tylko w³−i=0

Antonni: i³=i²*i= (−1)*i=−i Wtedy skorzystasz ze wzoru a³+b³ =

Dyb: ok już wszystko jest zrozumiałe dziękuje bardzo ICSP oraz Antonni

Mila: i³=i²*i=−i Zastąpiono (−i) liczbą (+i³) , wtedy możesz skorzystać z wzoru skróconego mnożenia , co ułatwi Ci rozwiązanie równania. ³√i nie jest rozwiązaniem. II sposób z³=i z=³√i |i|=1

	π
φ=
	2

	π   +2kπ) 2		π   +2kπ) 2
zk=1*(cos		+i sin		), Dla k∊{0,1,2)
	3		3

	π		π		√3		1
z0=(cos		+i sin		)=		+i *
	6		6		2		2

	5π		5π		√3		1
z1=(cos		+i sin		)=−		+i *
	6		6		2		2

	3π		3π
z2=cos		+i sin		=0−1i=−i
	2		2

Dyb: Dziękuje

Dyb: Zadanie już zrobiłem tylko, że I sposobem. Mila w II sposobie nie rozumiem skąd wzięło się |i|=1?

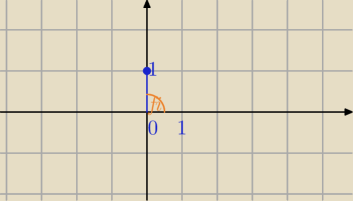
Mila: ³√i i=0+1i |i|=√0²+1²=1 Liczba (i) to punkt (0,1) na płaszczyźnie zespolonej.

Dyb: Bardzo ciekawy sposób

Mila: To przecież zwykła interpretacja geometryczna liczb zespolonych. http://www.matmana6.pl/tablice_matematyczne/studia/liczby_zespolone/140-definicja_i_interpretacja_geometryczna_liczby_zespolonej