Jakie warunki?
Hejo: Dla jakich wartości parametru m równanie x
2 −2mx +m
2 −1 = 0 ma dwa różne pierwiastki większe
od 1?
No to założenie jakie na pewno będzie
a=1≠0
1) Δ>0
Jakie będą pozostałe warunki? Dlaczego takie akurat?

12 paź 23:08
5-latek:
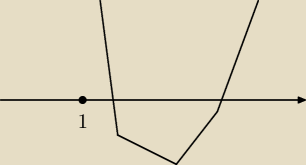
Ramiona paraboli w gore wiec f(1)>0
12 paź 23:11
Hejo: Hmm a skąd wiemy że dla argumentu 1 ramiona paraboli w górze? Te dwa warunki wystarczą?
12 paź 23:15
5-latek: wspolczynnik przy x2 jest dodatni stad w gore .
12 paź 23:17
Hejo: Rozumiem ale dlaczego oś symetrii paraboli za jedynką?
12 paź 23:19
Jack:
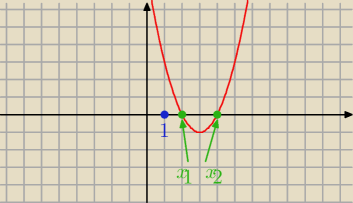
ramiona paraboli w gore, skoro ma 2 rozne pierwiastki i wieksze od jeden, to oznacza, ze kazdy
z pierwiastkow jest wiekszy niz 1.
x
1 > 1, x
2 > 1
wiec f(1) > 0
12 paź 23:20
Omikron: Możesz też
x1>1 i x2>1
x1−1>0 i x2−1>0
Jeżeli dwie liczby są dodatnie to ich iloczyn i suma są dodatnie.
(x1−1)(x2−1)>0 i x1−1+x2−1>0
Wzory Vieta.
Rozwiązanie przy wykorzystaniu wykresu jest jednak szybsze
12 paź 23:21
Jack: gdyby os symetrii byla przed jedynka albo w jedynce to nie mielibysmy spelnionego warunku
x1 > 1
x2 > 1
bo np. by bylo
x1 < 1 , x2 > 1
12 paź 23:21
zz: x1 * x2 <0 bo musza byc rozne
12 paź 23:23
myszka:
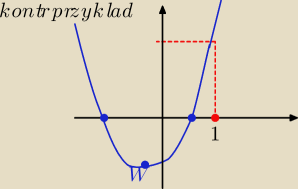
Aby spełnione były warunki w tym zadaniu to:
parametr "m" musi spełniać układ warunków:
1 / Δ>0
2/ f(1)>0
12 paź 23:23
piotr: Δ=4>0
(x1−1)(x2−1)>0 i x1 + x2 >2
⇒x1x2 − (x1+x2) > −1 i x1 + x2 >2
⇒c/a + b/a > −1 i −b/a > 2 ⇒ m>2
12 paź 23:25
Hejo: Z rozpatrywanych dwóch warunkach wyszedł zbiór (−
∞;0) U (2;+
∞)
Delta wyszła 4
4>0
więc R
f(1) = m(m−2) = 0
Z czego wyżej podany przedział
W odpowiedziach do zadania mam przedział (2;
∞)
Ktoś może mi wyjaśnić co robie źle?

12 paź 23:27
myszka:
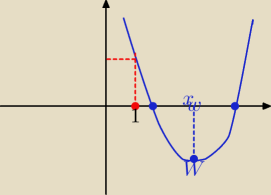
12 paź 23:27
Hejo: Aaa czyli brakowało mi jednego założenia na Xw. Dziękuję za rozchwianie wątpliwości
12 paź 23:29
piotr: (x1−1)(x2−1)>0 ⇒ (−∞;0) U (2;+∞)
x1 + x2 >2 ⇒ m>1
część wspólna: ⇒ m>2
12 paź 23:30
myszka:
Δ=4 ⇒ m∊R
f(1)>0 ⇒ m
2−2m>0 ⇒ m∊(−
∞,0)U (2,
∞)
teraz wybierz część wspólną
otrzymasz
Odp:
m∊(2,∞)
12 paź 23:31
Hejo: Dziękuję raz jeszcze, już rozumiem o co chodzi

12 paź 23:33
myszka:
Na zdrowie łap


12 paź 23:34
PW: Zawsze zanim zacznie się stosować schematy myślowe, warto się zastanowić, czy zadanie nie jest
łatwiejsze niż się wydaje na pierwszy rzut oka.
Równanie ma równoważną postać
(x − m)
2 = 1,
a więc rozwiązania spełniają warunki
x − m = −1 lub x − m = 1,
czyli dwa rozwiązania istnieją zawsze i są równe
x
1 = m −1, x
2 = m + 1,
a jeśli oba mają być większe od 1, to musi być spełniony układ nierówności
| | ⎧ | m − 1 > 1 | |
| | ⎨ | | ,
|
| | ⎩ | m + 1 > 1 | |
który spełniają liczby m > 2.
13 paź 00:30
Bogdan:
Pozdrawiam
myszkę 
i
PW 
13 paź 00:33
PW: Hej

chyba dawno Cię nie było, ze szkodą dla forum.
13 paź 00:35
Bogdan:
Dziękuję za mile słowa. Zaglądam tu od czasu do czasu, ale mniej się udzielam niz kiedyś.
13 paź 00:44
Metis: Szkoda

łezka się w oku kręci gdy czyta się Wasze poprzednie "wywody" matematyczne

13 paź 00:45

 Ramiona paraboli w gore wiec f(1)>0
Ramiona paraboli w gore wiec f(1)>0
 ramiona paraboli w gore, skoro ma 2 rozne pierwiastki i wieksze od jeden, to oznacza, ze kazdy
z pierwiastkow jest wiekszy niz 1.
x1 > 1, x2 > 1
wiec f(1) > 0
ramiona paraboli w gore, skoro ma 2 rozne pierwiastki i wieksze od jeden, to oznacza, ze kazdy
z pierwiastkow jest wiekszy niz 1.
x1 > 1, x2 > 1
wiec f(1) > 0
 Aby spełnione były warunki w tym zadaniu to:
parametr "m" musi spełniać układ warunków:
1 / Δ>0
2/ f(1)>0
Aby spełnione były warunki w tym zadaniu to:
parametr "m" musi spełniać układ warunków:
1 / Δ>0
2/ f(1)>0





 i PW
i PW 
 chyba dawno Cię nie było, ze szkodą dla forum.
chyba dawno Cię nie było, ze szkodą dla forum.
 łezka się w oku kręci gdy czyta się Wasze poprzednie "wywody" matematyczne
łezka się w oku kręci gdy czyta się Wasze poprzednie "wywody" matematyczne 