Rozwiąż
OLKA: Rozwiąż
1. |x|+|y|≥1
2. −x2 + y2 >4
3. |x|<1 i |y|<1
12 paź 15:21
Mila:
Napisz jakie polecenie masz w książce.
12 paź 15:38
OLKA: rozwiąż graficznie
12 paź 15:40
OLKA: rozwiąż graficznie
12 paź 15:41
Adamm:
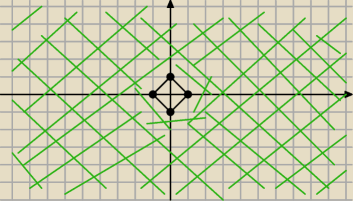
|x|+|y|≥1
na zielono jest obszar dla którego nierówność zachodzi
12 paź 15:58
PW: 3. Wskazówka.
|x| < 1 to równoważnie
(1) −1 < x < 1
− jest to zbiór takich par (x, y), w których pierwsza współrzędna x spełnia nierówność
(1), a druga jest dowolna. Ilustracją są dwie półpłaszczyzny bez wyznaczających je prostych.
Tak samo pomyśl o nierówności |y| < 1 i zobacz część wspólną tych zbiorów (część wspólną, bo
jest spójnik "i").
12 paź 15:59
PW: Doprecyzuję: Ilustracją jest część wspólna dwóch półpłaszczyzn (bo podwójna nierówwność (1) to
dwie nierówności połączone spójnikiem "i").
12 paź 16:02
Adamm:
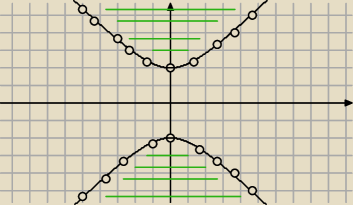
y
2−x
2>4
12 paź 16:07
Mila:
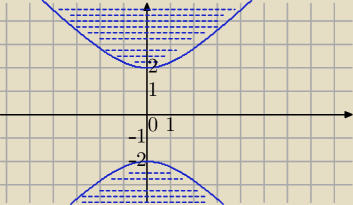
2)
|y|>
√x2+4
12 paź 16:07
Mila:
Tak, bez krzywych.
12 paź 16:08
Adamm:
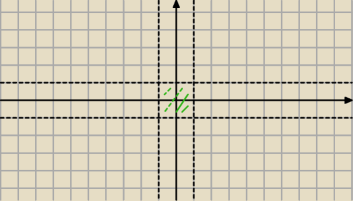
|x|<1 ∧ |y|<1
12 paź 16:10
 |x|+|y|≥1
na zielono jest obszar dla którego nierówność zachodzi
|x|+|y|≥1
na zielono jest obszar dla którego nierówność zachodzi
 y2−x2>4
y2−x2>4
 2)
|y|>√x2+4
2)
|y|>√x2+4
 |x|<1 ∧ |y|<1
|x|<1 ∧ |y|<1