Wyznacz ekstrema loklane... problem Macko z Bogdanca: Mam taki przyklad.... x³+8x²+21x+18 jesli x<−2 f(x)=

	x2−4
		jesli x≥−2
	x2+1

Robie to tak... f(x)=x³+8x²+21x+18 D_f= x∊(−∞,−2) D_{f '}⊂D_f x∊(−∞,−2) f '(x)=3x²+16x+21 Δ=256−4(63)⇒√Δ=2

	1
x1=−2		x2=−3
	3

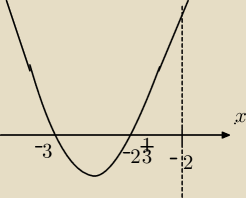
Szkicuje rysunek i otrzymuje: f_max (−3)=0

	1		−4
fmin (−2		)=
	3		27

Teraz robie drugi przypadek...

	x2−4
f(x)=
	x2+1

D_f x∊<−2,∞)

	(x2−4)'(x2+1)−(x2−4)(x2+1)'		10x
f '(x)=		=
	x2+1)2		(x2+1)2

D_{f '}⊂D_f x∊<−2,∞) f '(x)=0 10x=0 x=0.... Rysuje funckje linowa 10x ograniczona w przedziale <−2,∞) i otrzymuje f_min (0)=4 moje odpowiedz to: f_min (0)=4 f_max (−3)=0

	1		−4
fmin (−2		)=
	3		27

W ksiazce natomiast jest jeszcze podane f_max (−2)=0 Moglby ktos powiedziec sakd to sie bierze? Bo mi dla zadnego przypadku f '(x)=0 nie wychodzi x=−2

Adamm: oblicz pochodną dla x=2

Adamm: x=−2

Adamm: powiedz mi czy wyszła

Macko z Bogdanca:

	10x
hmmm f ' (x)=
	(x2+1)2

	−20		4
f '(−2)=		=−
	25		5

Chyba ze cos poplatlem, powinno pewnie wyjsc 0

Adamm: dla x=−2 mamy ciągłość, nie mamy tam pochodnej więc przeanalizujmy pochodne z obu stron lim_x→−2⁻f(x)=1 f(−2)=−0,8 znaki są różne więc mamy tam maksimum

Adamm: przy obu f powinien być apostrof

Macko z Bogdanca: Okej! rozumiem, dziekuje, nie pomysallem o tym !