pochodne studen:

	1
cześć, do narysowania mam wykres		,x∊(0,π)
	sinx

w związku z tym, że skończyłam lo kilka lat temu w mojej podstawie programowej nie było pochodnych i nie rozumiem jak to zadanie zostało na wykładzie rozwiązane. A mianowicie: x→0+ (dlaczego do 0+, czym to by się różniło od 0− i czy to jest takie odgórnie przyjęte, że szuakm dla tej liczby czy może chodzi o końce przedziałów/miejsca zerowe?) sinx→0+(dlaczego i dlaczego do 0+ i czym to się różni od 0−)

1
	→+∞
sinx

i potem to samo dla π x→π, sinx→0+

1
	→+∞
sinx

i na podstawie tego jest rysowany wykres, jednak nie mam pojęcia co i skąd się wzięło

Jack: dlatego do 0⁺ bo masz przedzial, ze x ∊(0 , π) zatem 0⁻ oraz 0 sie nie mieszcza w przedziale. no i potem x−>π (nie powinno byc π z minusem ?) bo tez do przedzialu nalezy. Czyli ogolnie to badasz konce przedzialow.

studen: a czym jest 0− a czym jest 0+? czym to się różni od siebie?

studen: i czym się różnią od zwykłego 0?

elo: to są granice, oznacza to że x zbliżają się do 0 od strony ujemne, bądź dodatniej

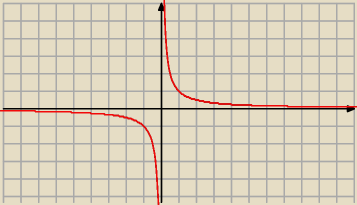
Jack: przy badaniu granicy 0⁻ oznacza, ze badamy jak idzie funkcja z lewej strony zera. natomiast 0⁺ to przy prawej stronie zera no a gdy granica przy lewej stronie zera = granica przy prawej stronie zera no to taka sama bedzie granica przy zerze zwyklym. Przyklad :

	1
wezmy sobie funkcje
	x

gdy badamy granice przy zerze z lewej strony (0⁻) to widzimy ze zbiega ona do − ∞ natomiast przy 0⁺ do + ∞ zatem ta funkcja nie ma granicy w zerze, ale z lewej i prawej strony ma granice jednostronne.

studen: ok, ale jeśli już podałeś taki przykład funkcji, to dlaczego przy 0+ zbiega ona do +∞? Mi się wydaje, że wraz ze wzrostem argumentów wartości funkcji maleją, więc zbiega ona do −∞

studen: aha, sekunda, badamy ją tak jakby idąc w stronę 0, tak? czyli w prawo w kierunku 0

Jack: tak, badasz ja patrzac na wykres idac w strone zera (no bo badamy w zerze)

studen: ok, to już zrozumiałam. Treaz jeszcze ostatnie pytanie−co to znaczy, że funkcja zmierza do 0+? Czyli tak jak ten mój przykłady, gdy x zmierza do 0+, to sinx zmierza też do 0+?

Jack: teraz gdy lim x−>0⁺ no to lim sinx przy x−>0⁺ to inaczej lim sin−>0⁺ a no sinus 0 stopni = 0 wiec granica

	1
lim		= +∞
	sinx

studen: nie rozumiem na razie w ogóle nie chcę używać limesów chcę to tylko w miaę łopatologicznie zrozumieć. Rozumiem, że gdy x→0+, to cała funkcja będzie zmierzała do 0, ale dlaczego do 0+? kiedy byłoby 0−?

Adamm: już ci to przecież wytłumaczyli człowieku, czytać umiesz x∊(0;π), nie idziemy do zera po ujemnych bo mamy ograniczenie przedziałem

studen: chodziło mi o funkcję, o sinx, nie o sam x

Adamm: 0<sinx<x dla x∊(0;π/2) znasz tą nierówność

Adamm: http://wazniak.mimuw.edu.pl/index.php?title=Analiza_matematyczna_1/Wyk%C5%82ad_5:_Obliczanie_granic tu masz opisane, poszukaj "Granice specjalne"

studen: znam, ale generalnie chodzi mi o coś innego w tym momencie. Zwykłe, lopatologiczne wyjaśnienie, bez zbędnych równań i nierówności

Adamm: przecież x ogranicza sinx, to czego innego może dążyć sinx, jak nie do 0

Adamm: oczywiście dla x→0⁺, czyli dla x>0, mamy sin(x)>0 więc sin(x) → 0⁺