trapez Tomm: Trapez o polu 18 √3 cm² i kątach ostrych 30^o i 60^o obraca się dokoła swej krótszej podstawy. Długość krótszej podstawy tego trapezu stanowi połowę długości dłuższej podstawy. Oblicz objętość i pole powierzchni całkowitej powstałej bryły.

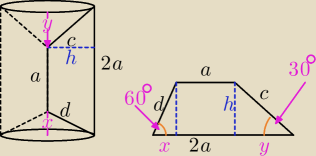
dero2005: a = 2b

2a+a
	*h = 18√3
2

3a
	*h = 18√3
2

h
	= tg60o = √3 ⇒h = x√3
x

h		√3		√3
	= tg30o =		⇒h = y
y		3		3

	√3
x√3 = y
	3

x+y = a x = a−y

	y√3
(a−y)√3 =
	3

	3
y =		a ⇒y = 36
	4

	1
x =		a ⇒ x = 12
	4

	1
h =		a√3
	4

wstawiamy do wzoru (trzeci wiersz)

3a		1
	*		a√3 = 18√3
2		4

a = 48 h = 12√3

h		1
	= sin30o =
c		2

c = 2h = 24√3

h		√3
	= sin60o =
d		2

d = 24

	1		1		y		x
V = πh2*2a −		πh2*y −		πh2*x = πh2(2a−		−		) =
	3		3		3		3

P_c = 2πh*2a + πhd + πhc = πh(4a + d + c) = dokoncz

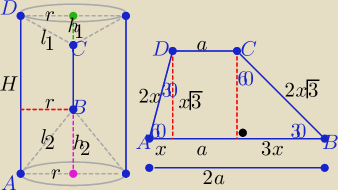
myszka: Ech dero2005 "mistrzu" od stereometrii Podaję taki sposób rozwiązania zadania ( dane na rysunku) h₁+h₂= a , H=2a , r= h

	1
V(br)= Vw−(Vst1}+Vst2) = πr2*H−		πr2(h1+h2)
	3

	1		5
V (br)= πr2*2a−		πr2*a ⇒ V(br)=		πr2*a
	3		3

P(br)= P_b(w)+P_b(st₁) +P_b(st₂) P(br)= πr( 2H+l₁+l₂) Z treści zadania i trójkątów "ekierek" o kątach 30^o,60^o, 90^o |AB|=2a= 8x i |DC|= a= 4x i h= x√3 , x>0 P_trapezu =18√3 ⇒ 6x*x√3=18√3 ⇒ x²=3 ⇒ x= √3 to H= 8x= 8√3 , r=h= x√3= 3 , a=4x=4√3 , l₁= 2x=2√3 , l₂=2x√3= 6 zatem : V= ........ = 60√3π [j³] P_c= ........= 18π(3√3+1) [j²]] ==============================================