gee adam: Jak obliczyc kąt miedzy przekątnymi w czworokącie A=(4,−3) B=(10,5) C=(9,9) D=(−2,10)

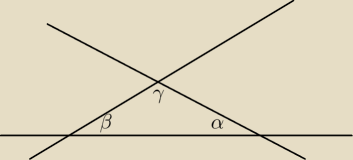
Adamm: możemy wyznaczyć te dwie proste, odpowiednie współczynniki to odpowiednie tangesy kątów, korzystamy z 180*=α+β+γ

myszka: 2 sposób ze wzoru na tgγ między prostymi AC i BD https://matematykaszkolna.pl/strona/1228.html

5-latek : Mozna rowniez napisac rownia prostych w postaci ogolnej 1..A₁x+B₁y+C₁=0 2. A₂x+B₂y+C₂=0 wtedy

	|A1B2−A2B1|
sinφ=
	√A12+B12*√A22+B22

	A1*A2+B1*B2
cosφ=
	√A12+B12*√A22+B22

	|A1*B2−A2*B1|
oraz tgφ=
	A1*A2+B1*B2

piotr:

	9−(−3)
współczynnik kierunkowy prostej AC:		= 12/5
	9−4

	10−5
współczynnik kierunkowy prostej BC:		= −5/12
	−2−10

proste są prostopadłe, kąt 90^o

myszka:

5-latek : piotr adam to student wiec powinien wiedziec ze ze wzoru 23 :06 cosφ=0 ma warunek prostopadlosci prostych A₁*a₂+B−1*B₂=0 natomiast ze zwiazku sinφ=0 ma zwiazek A₁B₂−A₂B₁=0 ktory stwierdza ze dane proste pokrywaja sie lub sa rownolegle

5-latek : Poprawiam warunek prostopadlosci A₁*A₂+B₁*B₂=0

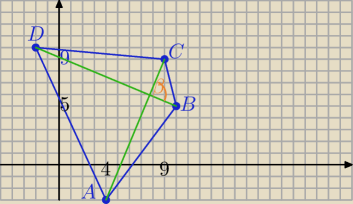
Mila: A=(4,−3) B=(10,5) C=(9,9) D=(−2,10) AC^→=[5,12] DB^→[12,−5] [5,12]o [12,−5]=5*12+12*(−5)=0 wartość iloczynu skalanego równa 0⇔ Przekątne są prostopadłe. II) Prosta AC: y=ax+b , potrzebujemy wsp. a

	9−(−3)		12
a=		=
	9−5		5

Prosta DB:

	5−10		−5
a'=		=
	10−(−2)		12

	12		5
a*a'=		*(−		)=−1⇔proste prostopadłe.
	5		12

β=90^o

5-latek : natomiast jesli ma rownania w postaci kierunkowej to oprocz tangensa miedzy prostymi moze rownie z wyznaczyc kat ze wzorow Majac wspolczynniki kierunkowe m₁ i m₂

	m1*m2+1
cosφ=
	√m12+1*√m22+1

	|m1−m2|
lub sinφ=
	√m12+1*√m22+1

Wzor na tangens kata miedzy prostymi podala myszka

daras: a co na to adam ?

Rafał: Ewentualnie można policzyć pole czworokąta, przedstawiając je jako sumę pól dwóch trójkątów o znanych wierzchołkach. Potem policzyć długości przekątnych i skorzystać ze wzoru

	1
P=		ef*sinφ, gdzie P to pole dowolnego czworokąta wypukłego, e i f to długości
	2

przekątnych a φ to miara kąta między tymi przekątnymi.