liczby zespolone kasia: z²=−i znajdź rozwiązania

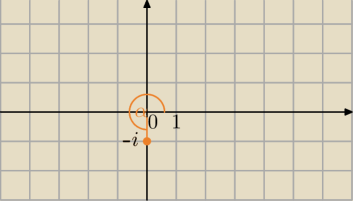
Mila: z=√−i (−i) to punkt (0,−1) na pł. zespolonej

	3π
α=
	2

|−i|=1

	3π   +2kπ 2		3π   +2kπ 2
zk=1*(cos		+i sin		) gdzie k∊{0,1}
	2		2

	3π		3π		√2		√2
z0=cos		+i sin		= −		+i
	4		4		2		2

	5π		5π		√2		√2
z1=cos		+i sin		=		−i
	4		4		2		2

kasia: dlaczego na początku omijasz pierwiastek i szukasz miejsca dla −1?

Mila: (−i) możesz zaznaczyć w układzie wsp. i odczytujesz argument, który jest potrzebny , aby wykorzystać podany wzór de Moivre'a. Nie zawsze tak łatwo to da się zrobić , ale w tym przypadku tak.

Mila: Argument liczby zespolonej http://www.math.edu.pl/argument-liczby-zespolonej Interpretacja geometryczna liczby zespolonej http://www.matemaks.pl/interpretacja-geometryczna-liczby-zespolonej.html http://www.matmana6.pl/tablice_matematyczne/studia/liczby_zespolone/140-definicja_i_interpretacja_geometryczna_liczby_zespolonej

Janek191:

	1 − i
− i = (		)2 = (U{ − 1 + i}{√2)2
	√2

więc

	1 − i		− 1 + i
√ − i =		lub √−i =
	√2		√2

Jack: kąt można wyznaczyć za pomocą sinusa i cosinusa

	Re
cos α
	|z|

	Im
sin α =
	|z|

α=...

Janek191:

	Re z
cos α =
	I z I

	Im z
sin α =
	I z I

Mila: Pewnie, że można, ale w niektórych przypadkach widzę od razu.