liczby zespolone
kasia: zaznacz na płaszczyżnie zespolonej rozwiązania rówania 28=1
nie wiem jak to ugryźć, zaczęłam tak:
28−1=0
28+i2=0
i nie wiem co dalej
6 paź 21:44
5-latek: Zeby sie za duzo nie rozpisywac to napisz definicje rownania .
6 paź 21:47
kasia: no wiem, że liczba zespolona musi się składać z liczby rzeczywsitej i urojonej, tylko nie wiem
jak z tego stworzyć tą urojoną
6 paź 21:48
Mila:
28≠1 coś zgubiłaś w zapisie.
6 paź 21:49
Jack: przeciez 28 = 1 to sprzecznosc
28 = 256
a 1 to 1
256 ≠ 1
nwm jak chcesz to zaznaczyc...
mozesz narysowac prosta y = 256, oraz prosta y = 1
ale ... co to da?
6 paź 21:50
5-latek: Zadalem Ci konkretne pytanie i oczekuje konktertnej odpowiedzi
Znajdziesz ja w ksiazce Jan Lesniak Rownania z jedna niewiadona .
6 paź 21:50
Andrzej: To jest 28 czy z8=1 ?
6 paź 21:51
kasia: oj kurcze sorry tam było z8=1
6 paź 21:51
Jack: Krzysiu,
jak widac nie kazdy wie, ze musi byc cos niewiadome zeby to obliczyc
6 paź 21:52
kasia: mimo wszystko dalej nie wiem jak to zrobić, może jakiś początek?
6 paź 21:57
piotr:
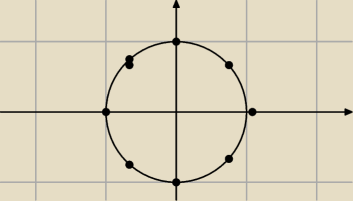
6 paź 21:59
5-latek: Witaj
Przeciez widac ze leci w kulki
Bedziesz mial do rozwiazania rownanie
(z
4+1)(z
4−1)=0
z
4−1=0 ma rozwiazania z=1 z=−1 z=i z=−i czyli wsystkie pierwiaski z jednosci stopnia
czwartego
Tobie zostawaim rozwiazanir rownania
z
4+1= (z
2−i)(z
2+i)=0
6 paź 22:00
Jack: ja to moge rozwiazac, ale na plaszczyznie to nie wiem... zaznaczyc po prostu punkty chyba.
no to widze kilka metod
albo bawienie sie wzorem a2 − b2 albo pierwiastkowanie.
ja wezme te pierwsza.
z8 − 1 = (z4 − 1)(z4 + 1) = (z2−1)(z2+1)(z4+1) = (z−1)(z+1)(z2+1)(z4+1)
zatem rozwiazania to
z = 1 lub z = − 1
z2 = − 1 −−−−> z2 = i2 −−−−−> z = i lub z = − i
z4 + 1 = 0 −−−−> z4 − i2 = 0 −>>> (z2−i)(z2+i) = 0
Teraz pomysl nad rozwiazaniami z2 − i = 0 oraz z2 + i = 0
6 paź 22:01
6 paź 22:05
5-latek: Jack
na plaszczyznie to zrobil
piotr
6 paź 22:07
Jack: ano czyli tylko punkty wystarczylo zaznaczyc.
rownanie
z4 + 1 ja bym jechal z trygonometrycznej.
6 paź 22:08
kasia: (z−i)(z+1)(z−1)(z+1)
dzięki
6 paź 22:12
5-latek: Jack
ja nie wiem jak wy to teraz liczycie ale z etgo wzoru co CI wyslalem skany (strona 34(na samyn
dole
Na stronie 35 masz obliczone pierwiastki kwadratowe z liczby i a takze z liczby (−i)
Zajrzyj sobie tam
6 paź 22:14
kasia: musze jeszcze te 8 rozwiążań zapisać w postaci algebraicznej
6 paź 22:17
Mila:
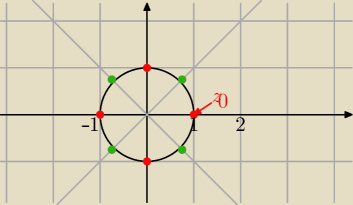
z
8=1
z
0=1
Pierwiastki rozłożą się tak jak na rysunku i koniec zadania
albo obliczenia
1)
Obliczenia ;
z
8−1=0
(z
4−1)*(z
4+1)=0⇔
(z
2−1)*(z
2+1)*(z
4−i
2)=0
(z−1)*(z+1)*(z
2−i
2)*(z
2−i)*(z
2+i)=0
z=1 lub z=−1 lub z=i lub z=−i lub
z2=i lub z2=−i
te ostatnie 4 pierwiastki odczytaj z wykresu albo rozwiąż:
z=
√−i i z=
√i
II sposób
z=
8√1
|1|=1
8√1=1
φ=0
z
0=1
| | 2kπ | | 2kπ | |
zk=1*(cos |
| +i sin |
| ) dla k=1,2,3,4,5,6,7 |
| | 8 | | 8 | |
| | π | | π | | √2 | | √2 | |
z1=cos |
| +i sin |
| = |
| +i |
| |
| | 4 | | 4 | | 2 | | 2 | |
| | π | | π | |
z2=cos |
| +i sin |
| =0+i*1=i |
| | 2 | | 2 | |
itd
6 paź 22:22
5-latek: W postaci algebraicznej rozwiazania beda takie
z
1=1
z
2=−1
z
3=i
z
4=−i
6 paź 22:40
Jack: Milu
A czy mozna to po prostu wziac "na logike"
skoro z8 = 1
to oznacza ze odleglosc od punktu (0,0) = 1 i ma byc 8 takich rozwiazan, zatem
rozpatrujemy okrag i zaznaczamy te 8 punktow w rownej od siebie odleglosci.
6 paź 22:50
Jack: chyba ze wlasnie to napisalas w poscie 22:22 w pierwszej czesci
6 paź 22:52
Mila:
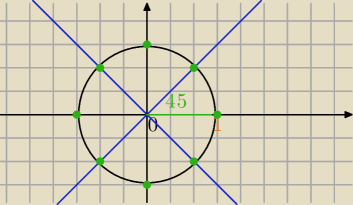
Tak, napisałam w pierwszej części , począwszy od z
0 co 45
o .
Znajdę teorię to prześlę linka.
6 paź 23:14
Jack: oki
6 paź 23:19