geo adam: napisz równanie okregu o promieniu 2√5 stycznego do prostej x−2y−2=0 w punkcie A którego rzędna wynosi −2

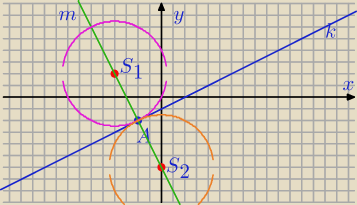
Adamm: istnieją dwa takie okręgi możesz wyznaczyć równanie wyznaczając prostą prostopadłą do x−2y−2=0 przecinającą się w A, punkty na prostej o odległości 2√5 od A to środki okręgów

adam: wiem, ale długim układzie równan i delcie wyszly mi inne wyniki niz w odpowiedziach

Mila: Jaką masz odpowiedź?

Mila: r=2√5 k: x−2y−2=0 A=(−2,b) środek okręgu leży na prostej prostopadłej do k w punkcie A −2−2b−2=0 −2b=4 b=−2 A=(−2,−2) m⊥k m: 2x+y+C=0 i 2*(−2)−2+C=0⇔C=6 m: 2x+y+6=0⇔y=−2x−6 S=(x₀,−2x₀−6) d(S, k)=2√5, k: x−2y−2=0

|x0−2*(−2x0−6)−2|
	=2√5
√1+4

|x₀+4x₀+12−2|=2*5 |5x₀+10|=10⇔ 5x₀+10=10 lub 5x₀+10=−10 5x₀=0 lub 5x₀=−20 x₀=0 i y₀=−6 lub x₀=−4 i y₀=−2*(−4)−6=2 S₂=(0,−6) lub S₁=(−4,2) x²+(y+6)²=20 lub (x+4)²+(y−2)²=20

adam: Dzieki

Mila: