przebieg zmienności funkcji Aga: zbadaj przebieg zmienności funkcji f(x)=x/lnx −ekstrema −monotoniczność −punkty przegięcia −wypukłość

Aga: pomoże mi ktoś?

Aga: znajdzie się ktoś miły?

Aga: znajdzie się ktoś miły?

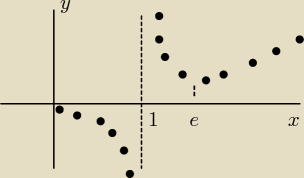
AS: Znalazł się!

	x
Dana funkcja f(x) =
	lnx

1. Dziedzina: x > 0 2. Asymptota pionowa lnx = 0 ⇒ x = e⁰ = 1 Asymptota pionowa: x = 1 3. Wartości dodatnie i ujemne funkcji

	x
f(x) > 0 ⇔		> 0 ⇔ x > 0 i lnx > 0 ⇔ x > 0 i x > e0 ≈ x > 1 ⇔ x > 1
	lnx

Funkcja przyjmuje wartości dodatnie dla x > 1

	x
f(x) < 0 ⇔		< 0 ⇔ x > 0 i lnx < 0 ⇔ x > 0 i x < 1
	lnx

Funkcja przyjmuje wartości ujemne dla 0 < x < 1 4. Granica − stosuję regułę L'Hospitala

	x		1
lim(x→∞)		= lim(x→∞)		= lim(x→∞)(x) = +∞
	lnx		1/x

Wartości funkcji zmierzają do +∞ gdy x → +∞ 5. Ekstremum funkcji

	1*lnx − x*1/x		lnx − 1
f'(x) =		=
	(lnx)2		(lnx)2

Warunek ekstremum: f'(x) = 0 f'(x) = 0 ⇔ lnx − 1 = 0 ⇔ lnx = 1 ⇔ x = e¹ ⇔ x = e Wartość ekstremum

	e		e
f(e) =		=		= e
	lne		1

Ekstremum funkcji znajduje się w punkcie W(e,e) 6. Przedziały wzrastania i malenia funkcji f'(x) > 0 ⇔ lnx − 1 > 0 ⇔ lnx > 1 ⇔ x > e Funkcja wzrasta dla x > e f'(x) < 0 ⇔ lnx − 1 < 0 ⇔ lnx < 1 ⇔ x < e Funkcja maleje w przedziałach (0,1) U (1,e) x 0 1 e +∞ −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− f(x) 0 ↘ −∞|+∞ ↘ e ↗ +∞ min

Jacek: x³+6*x²

Godzio: Mała poprawka: D = (0,1)∪(1,∞)

Julaa: Czyli ta funkcja: −nie jest parzysta −nie jest nieparzysta −nie jest okresowa ? I czy coś zmienia w obliczeniach to, że D = (0,1)∪(1,∞) a nie x>0 ?

Artur z miasta Neptuna: Tak, tak i tak oczywiscie ze zmienia −−−− patrz asymptota

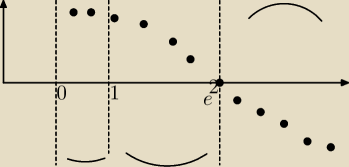
Kuba: odnośnie wypukłości y''={−lnx+2}/{x(lnx)³} y''=0=−lnx+2 2=lnx x=e² wykres zaczyna się od dołu bo największa potęga x lnx jest ujemna czyli wypukła jest od x∊(e²;∞) i wklęsła x∊(0;e²) / 1 a na wykresie jest przeciwnie i chciałbym wiedzieć co robię źle