Styczne, pochodne MJay: Nie mam kompletnie pojęcia jak to zrobić: Dana jest funkcja kwadratowa f określona wzorem f(x)=x² i punkt P = (p,p²) leżący na wykresie tej funkcji, gdzie p jest dowolną liczbą rzeczywistą. Wyznacz a i b tak, by prosta o równaniu y=ax+b była styczna do wykresu funkcji f w punkcie P. Wykaż, że dla każdego x zachodzi nierówność x² ≥ ax+b

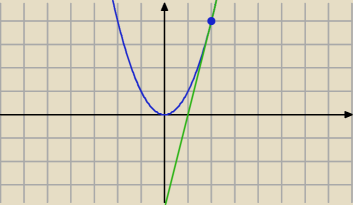
Janek191: f '(x) = 2x a = f '(p) = 2p y = 2p x + b p² = 2p*p + b b = − p² Odp. y = 2p x − p² =============== Np. P = ( 2, 4) Wtedy y = 4 x − 4

Jack: Prosta styczna do funkcji : a = f ' (x₀) skoro ma byc styczna w punkcie P no to f ' (p) = a f(p) = p² f ' (p) = 2p = a zatem funkcja ma rownanie y = 2p * x + b podstawiamy dane punktu P p² = 2p * p + b p² = 2p² + b − p² = b zatem prosta ma rownanie y = 2px − p². mamy teraz wykazac, ze x² ≥ ax + b czyli inaczej, x² ≥ 2px − p² przeksztalcajac rownowaznie x² − 2px + p² ≥ 0 (x−p)² ≥ 0 a to jest spelnione dla kazdej x ∊ R