Funkcja liniowa Izydor: Miejsca zerowe dwóch funkcji liniowych są liczbami odwrotnymi. Wykresy tych funkcji przecinają się w punkcie (0,3) i wraz z osią OX ograniczają trójkąt o polu 4. Wyznacz wzory tych funkcji.

	8		8		1
Rozumiem, że cała podstawa trójkąta ma		, czyli		=|a−		|
	3		3		a

Ktoś mógłby pomóc?

Ajtek: Wygląda okej.

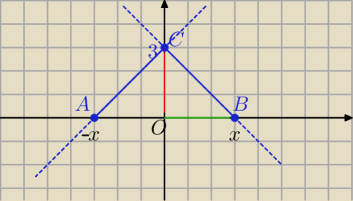myszka: A( −x,0) B(x,0) C(0,3)

	1		4
P(OBC)= 2 ⇒		*x*3=2 ⇒ x=
	2		3

	4		4
A(−		,0) B(		,0)
	3		3

równania tych prostych : ........ już sam dokończ

myszka:

	9
BC: y= −		x+3
	4

	9
AC : y=		x+3
	4

Izydor: Dziękuje za pomoc myszka ale chodziło tutaj o liczby odwrotne a nie przeciwne. Postaram się tą wartość bezwzględną jutro wyliczyć na spokojnie jeszcze raz, może wyjdzie mi z tego coś sensowniejszego ale byłbym też bardzo wdzięczny gdyby ktoś w razie czego pomógł mi tutaj ją rozwiązać .

5-latek: Z rysunku wychodzi pole 9j² a ma byc 4j²

Ajtek: myszka, liczby odwrotne, czy przeciwne Z treści zadania wynika że odwrotne .

5-latek: Jakos Ajtek wszyscy ostatnio nie maja czasu i wstawiaja zadania bardzo pozno wiec łatwo o pomylke

5-latek: Nalezy rozwiazac rownie

	1		1
4=		*3*|a−		|
	2		a

myszka: Sorry źle przeczytała treść zadania Poprawiam się Proste mają równania : y=nx+3 i y= mx+3 i h=3

	1		8		1		8
P=		a*h ⇒ 3a=8 to a=		a= |x−		| =		i x≠0
	2		3		x		3

	x2−1		8
to: |		|=		⇒ 3(x2−1)= 8x lub 3(x2−1)= −8x
	x		3

3x²−8x−3=0 lub 3x²+8x−3=0 , Δ=100 , √Δ=10

	1		1
x= 3 v x= −		v x= −3 v x=
	3		3

zatem n*3+3=0 ⇒ n= −1 −3n+3=0 ⇒ n= 1 lub

	1		1
m*(		)+3=0 ⇒ m= −9 −		m+3=0 ⇒ m= 9
	3		3

są dwie pary takich prostych: 1/ y= −x+3 i y= −9x+3 lub 2/ y= x+3 i y= 9x+3

myszka:

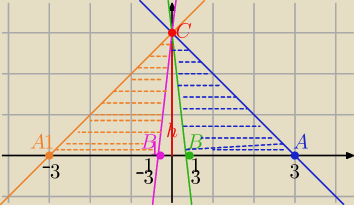
5-latek: myszka Moje rownanie jest dobre ?

myszka:

	1
Dobre ( tylko ,że ja wprowadziłam inne oznaczenia z miejscami zerowymi x i		)
	x

5-latek: Dziekuje CI bardzo

5-latek: Dobranoc