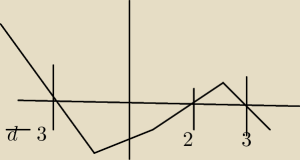
qeqweqw Krzysiek: Przyklad z internetu

	√x2−5x+6
f(x)
	x2−9

pierwiastek jest 4 stopnia wg tego co mialem na zajeciach mianownik musi byc rozny od zera x²−9 ≠ 0 (x−3)(x+3) ≠ 0 x ≠ 3 n x ≠ −3 x²−5x+6 ≥ 0 delta = 1; x1=2; x2=3 D = (−oo, −3) u <2,3) u (3,+00)

PW: A może zamiast swoich rozważań napiszesz treść zadania? Rysunek nie wiadomo do czego służy. Czyżbyś pytał o qeqweqw?

Krzysiek: @PW, zapomniałem.Przepraszam.Chodzie o dziedzine oczywiście

Adamm: obliczenia dobre, dziedzina jakimś cudem zła

Adamm: D=(−∞;−3)u(−3;2>u(3;∞)

Krzysiek: nie rozumiem tego za bardzo. a od <2,3)?

Adamm: jakie jest rozwiązanie x²−5x+6≥0 twoim zdaniem ?

Krzysiek: a moze z wykresem cos nie tak

Krzysiek: sekundka

Krzysiek: D=(−∞;−3)u(−3;2>u <2,3) U(3;∞)

Krzysiek: a ... nie, parabole tworze tak?

Krzysiek: i tak pod spodem to już nie jest zawierane, bo to wartości ujemne , a w R nie ma pierwiastkow z liczb ujemnych

Krzysiek: powinno być D=(−∞;−3)u(−3;2>u(3;∞)

Krzysiek: zgadza się?

Adamm: przecież tak napisałem

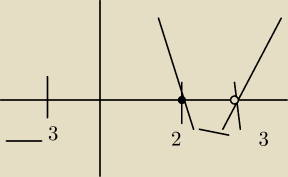
Krzysiek: NIe nie. To ja wiem , że dobrze napisałeś. Pytam się, czy to co napisałem z parabolą sie zgadza.

Krzysiek: Chodzi mi o to, że nie rysuje takich 'zygzakow' tylko w ten sposob

Krzysiek: Nie wiem po co rysowalem te zygzaki wyzej. W poprzednich przykladach tak bylo, i mi dziedzina wychodzila, tutaj nie rozumiem kiedy sie to robi , a kiedy nie

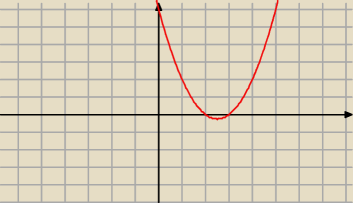
Adamm: parabola na rysunku to ta twoja odpowiedz sam sobie

Krzysiek: No chyba tak, inaczej nie zgadzaloby sie moje rozwiazanie z twojim

Krzysiek: Musze się zastanowić i przejżec poprzednie

Krzysiek: Tak. Zastanowilem sie, wiem gdzie miale luki w mysleniu.