geo tym: napisz równanie stycznej do okregu x²+y²=4 przechodzacej przez punkt A=(4,0)

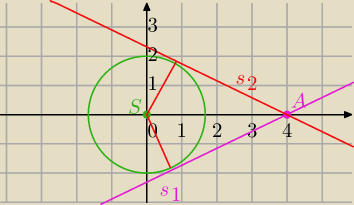
Mila: S=(0,0) środek okręgu. Odległość stycznej od środka okręgu jest równa długości promienia. Styczna s: y=ax+b i A∊s⇔a*4+b=0, b=−4a s: y=ax−4a przekształcamy do postaci ogólnej ax−y−4a=0

	|a*0−0−4a|
d(S,s)=2=
	√a2+1

|4a|=2*√a²+1 /² 16a²=4*(a²+1) 12a²=4

	1
a2=
	3

	1		1
a=		lub a=−
	√3		√3

	1		4
s1=		x−
	√3		√3

lub

	1		4
s2=−		x+
	√3		√3

===============

tym: dzieki

Mila:

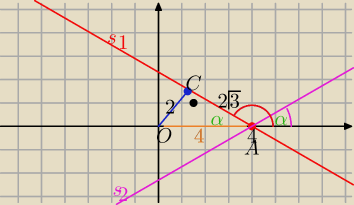myszka: 2sposób A trójkącie OAC : |OA|=4 , |OC|=2 , to |AC|=2√3 zatem: α= 30^o lub α= 180^o−30^o= 150^o

	√3		√3
a2=tg30o =		, a1= tg150o = −
	3		3

	√3		4√3
s1: y= a1(x−xA) ⇒ s1 : y= −		x+
	3		3

	√3		4√3
s2 : y= a2(x−xA) ⇒ s2 : y=		x−
	3		3