Pochodne, problem z monotonicznoscia Macko z Bogdanca: Pochodne, problem z monotonicznoscia Mam takie zadanie

	x2−4
		jesli x<2
	x2+2

f(x)= x³−2x² jesli x≥2

	12x
Licze pochodne kolejno:		, 3x2−4x
	x2+2)2

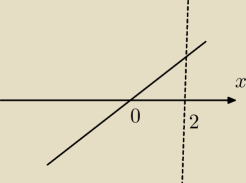
Wiemy, ze D_f'=R Rozwazam sobie najpierw przedzial x<2 Robie tak: zapisuje f'(x)=0 ⇔ (12x)(x²+2)²=0 Rysuje sobie wykres jak wyzej... f '(x)>0 ⇔ x∊ (0,2) oraz f '(x)>0 ⇔ x∊ (−∞,0) Sprawdzam ciaglosc funkcji w puncie x₀=0

lim
	f '(x)=0
x→0+

lim
	f '(x)=0
x→0−

f '(0)=0

lim
	f '(x)=f '(0)=0....
x→0

Okej teraz zabieram się za x≥2 f '(x)=3x²−4x

	1
Δ=4 x1=0 x2=1
	3

rysuje parabole z ramionami skierowanymi w gore... (rozpatruje oczywiscie od argumentu 2) otrzymujemy f '(x)>0 ⇔ x∊(2,∞) Noi teraz sprawdzam analogicznie jak dla punktu 0 ciaglosc funkcji w punkcie x₀=2

lim
	f '(x)=0
x→2+

lim
	f '(x)=2/3
x→2−

f '(2)= dla pochodnej x<2 otrzymuje 2/3 a dla x≥2 otrzymuje 0 Wynik ma byc. maleje dla (−∞,0> rosnie dla <0.∞) Niby wszystko by wychodzilo tylko nie wiem czy ta funckja cjest ciagla w punkcie 2? Mi niby wychodzi ze nei jest chyba ze czegos nie widze...

Macko z Bogdanca: oraz f '(x)<0 ⇔ x∊ (−∞,0)*

Adamm: po co ciągłość dla 0

Macko z Bogdanca: No faktycznie nie potrzbnie, to liczylem a co z 2?

Adamm: po 2. co ma ciągłość do monotoniczności

Adamm: porównaj lim_x→2⁻ f(x) oraz f(2)

Macko z Bogdanca: Z tego co mysle ze wiem to ciaglosc funkcj iw zbiorze decyduje o tym czy mozemy domknac przedzialy np gdy mamy ciaglosc w zbiorze R to mozemy zapisac zamiast (−∞,2) (−∞,2> gdyby funckcja nie byla ciagla w pkt 2 to musielisbymy zostawic (−∞,2) Dobrze mysle?

Adamm: nie

Adamm: jeśli pochodna drugiej f. jest nieujemna dla x≥2 oraz lim_x→2⁻f(x)<f(2) to f. jest rosnąca dla x≥0, rozumiesz

Adamm: nawet jeśli jest mały przeskok to jeśli nadal pozostaje rosnąca to jest wszystko ok

Adamm: przy lim f(x) < f(2) powinno być ≤

Macko z Bogdanca: Kurcze to juz nie wiem.... Cytat z ksiazki.... f ' (x) =15x²−15x⁴ D_{f '}=R f ' (x)>0 ⇔ x∊ (−1,0)U(0,1) f ' (x)<0 ⇔x∊(−∞,1)U(1,∞) Ponadto funkcja f jest ciagla w zbiorze R Zatem jest ona rosnaca w kazdym z przedzialow <−1,1> i <0,1> oraz malejaca w kazdym z przedzialow (−∞,−1>,<1,+∞) Zauwazamy ze przedzialy w ktorych funkcja f jest rosnaca maja wspolny koniec pkt 0 Tzn ze funkcja f jest rosnaca w sumie tych przedzialow czyli <−1,1> Noi powiedzmy ze gdyby funckja byla ciagla w zbiorze R−(1) to dalej byly by przedzialy domkniete?..

Adamm: jeśli byłaby w tych punktach zdefiniowana oraz te punkty zgadzałyby się z monotonicznością tzn. f maleje dla x∊(1;∞) czyli jeśli f(1)<lim_x→1⁺ f(x) to wszystko byłoby w porządku

Adamm: ale wtedy rosnąca nie byłaby dla x∊<−1;1>

Macko z Bogdanca: Ok, dziekuje, pomysle nad tym