GEOMETRIA neverbenance: W trapez prostokątny ABCD (AD prostopadłe do AB) o krótszej podstawie DC równej 3 wpisano okrąg o środku w punkcie O i promieniu równym 2. a) udowodnij, że trójkąt BOC jest prostokątny b) oblicz stosunek promienia okręgu wpisango do promienia okręgu opisanego na trójkącie BOC

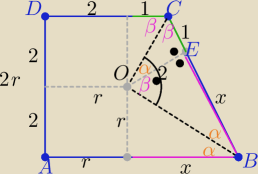
myszka: a) Środek okręgu wpisanego w trapez znajduje się w punkcie przecięcia dwusiecznych kątów ABC i DCB to 2α+2β=180^o ⇒ α+β=90^o |∡BOC|= α+β= 90^o c.n.w b) z podobieństwa trójkątów BOE i COE z cechy (kkk)

	|OE|		|BE|
		=		⇒ |OE|2= |CE|*|BE| ⇒ 4=1*x ⇒ x=4
	|CE|		|OE|

to |OC|= √2²+1²= √5 i |OB|=√2²+4²= 2√5 w trójkącie prostokątnym BOC : |BC|= 5

	1
R(wp) =		|BC|= 2,5
	2

	|BO|+|CO|−|BC|
r(op)=		= .......
	2

R
	=.......
r

teraz tylko dokończ obliczenia ...

myszka: I jak? ......

Janek191: Myszka ( czytaj Eta ) powinna wydać zbiór zadań z planimetrii z rozwiązaniami

5-latek: janek191 Ale nie wiadomo czy ta myszka to Eta Jak wiesz to Eta albo myszka a tutaj jest kolor bardziej zloty . No chyba ze ją mąz ozłocił i zmieniła kolor

myszka: