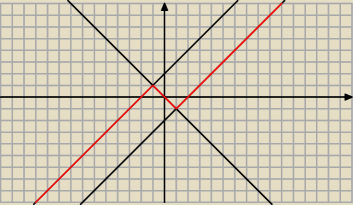
pomocyyy heyyy: Naszkicuj wykres funkcji

	⎧	x+2 dla x∊(−∞,−1)
f(x) =	⎨	−x dla x∊<−1,1>
	⎩	x−2 dla x∊(1,+∞)

a) Oblicz miejsca zerowe funkcji f oraz współrzędne punktu wspólnego wykresu funkcji f i osi OY. b) Wyznacz algebraicznie zbiór tych argumentów, dla których funkcja f przyjmuje wartości nieujemne. c) Oblicz wartość funkcji f dla argumentu 6. d) Naszkicuj wykres funkcji y = f(x) i na jego podstawie naszkicuj wykres funkcji g(x) = f(–x); omów własności funkcji y = g(x).

zef:

klkl: czy w podpunkcie b takie rozumowanie jest dobre: x+2≥0 −x≥0 x−2≥0 więc z tego wychodzi że wartości nieujemne przyjmuje on gdy x∊<−2,0>∪<2,+∞) ?

Adamm: dla x+2≥0 rozwiązanie ograniczasz do x∊(−∞;−1) etc.

zef: x+2≥0 −x≥ x−2≥0 To jest ok tylko pamiętaj aby uwzględnić przedziały tych 3 funkcji

Adamm: czyli dobrze

zef: Adamm jesteś studentem czy jeszcze szkoła średnia ? Pytam z ciekawości

Adamm: średnia, ale już niedługo

zef: Z tego co zauważyłem to chyba już kończysz materiał ze szkoły średniej i już uczysz się na własną rękę patrząc na niektóre zadania które rozwiązujesz Jak radzisz sobie z całkami i zespolonymi ?

Adamm: jeśli chodzi o całki to oznaczone, nieoznaczone, z funkcji wymiernych etc. umiem ale jeszcze mam zamiar się douczyć, a jeśli chodzi o zespolone to nie bardzo (praktycznie nic na ten temat nie robiłem, chociaż rozumiem to u podstaw)

zef: A jak z materiałem maturalnym, uważasz że już wszystko przerobiłeś ? Robiłeś działy szybciej niż w szkole ?

Adamm: nie, chociaż pochodne oczywiście oraz trochę prawdopodobieństwa już znam

klkl: czyli nie mogę tego napisać jako sumy przedziałów dla całej funkcji, tylko zbiór argumentów dla kazdego przedziału odpowiednio do tego co miałam w treści zadania? czyli:

	⎧	x≥−2 dla x∊(−∞,−1)
f(x)≥0 <=>	⎨	x≤0 dla x∊<−1,1>
	⎩	x≥2 dla x∊(1,+∞)

?

zef: Już myślałem że wszystko za tobą patrząc po tych trudniejszych zadaniach. Pozdrawiam

zef: Możesz to zapisać jako suma przedziałów tej funkcji. Twoja funkcja dzieli się na pewne przedziały ale to nic nie zmienia.

Adamm: tak szczerze mówiąc to uczę się matmy, ale to co podają w szkole jest dla mnie mniej ciekawe niż to co mogę znaleść na własną rekę