Optymalizacja artex: Jaką największą objętość może mieć bryła powstała z obrotu trójkąta równoramiennego o obwodzie 36 wokół podstawy trójkąta.

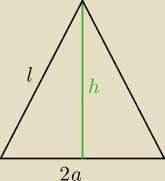
===: 2l+2a=36 ⇒ l+a=18 ⇒ l=18−a h=√l²−a²=√(18−a)²−a²=√324−36a=6√9−a W wyniku obrotu wokół podstawy (2a) powstaną dwa stożki o promieniu podstawy h i wysokości a Ich objętość to

	1
V=2*		π(324−36a)a
	3

	2π
V'=		(−72a+324)
	3

V'=0 72a=324 ⇒ a=4,5 V_max=V(4,5)= ...

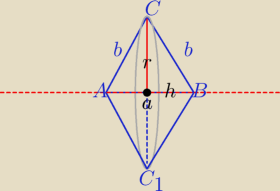Mila: a+2b=36⇔a=36−2b, 0<b<18 V_f=2*V_s

	1
Vs=		π*r2*h
	3

	1		1
h=		a=		*(36−2b)=18−b,
	2		2

r²=b²−h²

	1
r2=b2−(		a)2⇔r2=b2−(18−b)2
	2

r²=36*(−9+b)

	1
Vs=		*π*36*(−9+b)(18−b)=12π*(−162+9b+18b−b2)
	3

V_s=12π* (−b²+27b−162) parabola skierowana w dół wsp. wierzchołka

	−27		27
bw=		=
	−2		2

	27		27		27		81
Vs(		)=12π*(−9+		)*(18−		=12π*		=243π
	2		2		2		4

V_f=486π ===== Posprawdzaj rachunki

===: ... wynik ten sam czyli OK

Mila: Oczywiście, ja jak zwykle rozciągam pisanie Pozdrawiam.

===: