Równanie wykładnicze z parametrem Magda: Zbadaj liczbę rozwiązań równania w zależności od wartości parametru m ∊ R 2^|x−2|+x = m² Lewa strona jest dodania, a prawa nieujemna, czyli dla m=0 nie będzie rozwiązań, ale na tym moja koncepcja się kończy...

PW: A ja mam koncepcję, że wszystkie x ≤ 2 są rozwiązaniami dla m = 2.

Mila: Najlepiej graficznie.

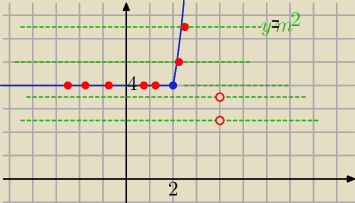
myszka: Rysujemy wykres: y=2^|x−2|+x i wykres y= m² nieskończenie wiele rozwiązań dla m²=4 ⇒ m= 2 v m= −2 1 rozwiązanie dla m²>4 ⇒ m∊(−∞, −2) U (2, ∞) 0 rozwiązań dla m²<4 ⇒ m∊(−2,2)

Mila: dla myszki.

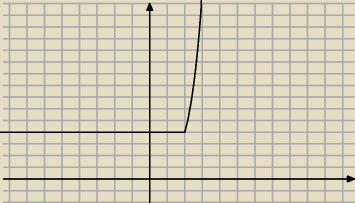
5-latek : Dla x<2 funkcja ma postac y= 2^2−x+x= 2²=4 Dka x≥2 funkcja ma [postac y= 2^x−2+x= 2^2x−2 =4^x−1 (to sa tylko przeksztalcenia proste TO jest wykres tej funkcji

myszka: dla Mili

PW: A już tak "kawę na ławę", gdy Magda miała zalążek koncepcji

myszka: O "zalążkach" ...... dzisiaj było najgłośniej

Mila: Nie widziałam Twojej koncepcji i też się wtrąciłam. Piszemy, a za chwilę 5 wpisów. Dobranoc wszystkim

myszka: Miłych snów

Magda: O, i wszystko jasne! Muszę się, widać, przekonać do graficznych rozwiązań zadań− bardzo wszystkim dziękuję!