promień okregu wpisanego
bas890: W trójkącie równoramiennym ramię ma długość 8 a kąt nachylenia ramienia do podstawy ma miarę
30stopni . Oblicz długość promienia okręgu wpisanego w ten trójkąt
Proszę o pomoc

8 sty 18:46
justyna: wyznaczasz wpierw długość podstawy, następnie z pitagorasa wyliczasz wysokość trójkąta.
średnica to 2/3 wysokości
8 sty 19:05
bas890: nie bardzo rozumiem mozna bardziej jasniej prosze

8 sty 19:08
justyna: z sinusa bąć cosinusa wyznacz długość podstawy trójkąta, mając podstawę i boki możesz wyliczyć
wysokość trójkąta ( połowa podstawy do kwadratu + wysokość do kwadratu = 82), średnica okręgu
to 1/2 promienia, średnica wynosi 2/3 wysokości trójkąta
8 sty 19:16
bas890: juz mam zrobione wlasnie to zadanie ta metoda chcialam sie zapytac czy mozna jeszcze inna
metoda je rozwiazac?
czy mozna skorzystac z wlasnosci 30 60 90 stopni

8 sty 19:24
justyna: nie znam jej
ale tutaj nie ma kątów 60 i 90 stopni, bo to trójkąt równoramienny
8 sty 20:16
bas890: a mozna jeszcze inna metoda rozwiazac to zadanie nasza nauczycielka powiedziala ze sie da
9 sty 13:05
justyna: ale jaką? jakimi 'metodami' Wy to robicie?
9 sty 13:15
justyna:
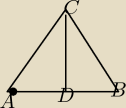
mogłabyś wyliczyć wysokość z tej metody 30,60,90 chociaż nie pamiętam o co z nią chodziło. kąt
DAC ma miarę 30 , ACD 60 (bo wysokość dzieli kąt 120 na połowę), CDA 90. I długość AC to 8
9 sty 13:19
bas890:
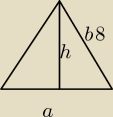
α=30stopni
cosα=
12a/b
√3/2=
12a/b
a=8
√3
P=
12ab*sinα=
12*8
√3*8*
12=16
√3
P=
12(a+2b)r
r=
2Pa+2b=2*16
√3/8
√3+16=4
√3(2−
√3)
odp. r=4
√3(2−
√3)
My to tak zrobiliśmy a jak inna metoda zrobic prosze o pomoc

9 sty 16:16
R.W.16l:
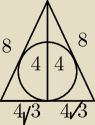
W trójkącie równoramiennym ramię ma długość 8 a kąt nachylenia ramienia do podstawy ma miarę
30stopni . Oblicz długość promienia okręgu wpisanego w ten trójkąt
Podstawa ma długość 8
√3
h=4
9 sty 16:27
bas890: tylko ze wynik ma wyjsc taki r=4√3(2−√3)

9 sty 16:50
Eta:
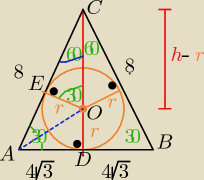 2/ sposób
2/ sposób
h= 4 IOCI = h−r= 4−r IACI= 8 IADI = 4
√3
ΔADC ~ Δ OEC z cechy ( k,k,k)
to;
to 4
√3( 4−r)= 8r /:4
4
√3−
√3*r = 2r => 2r +
√3r= 4
√3 => r( 2+
√3)= 4
√3
to
| | 4√3 | | 4√3(2−√3) | | 4√3(2−√3) | |
r= |
| = |
| = |
|
|
| | 2+√3 | | (2+√3)(2−√3) | | 4 −3 | |
to
r= 4√3(2 −√3)
3/ sposób też jest ...... ( ale trzeba umieć wyznaczyć tg15
o )

miara kąta DOA = 15
o bo OA zawiera się w dwusiecznej kąta 30
o
to z ΔDAO mamy:
to r = 4
√3*tg15
o
| | tgα− tgβ | |
ze wzoru na tg( α−β)= |
|
|
| | 1 +tgα*tgβ | |
| | tg45o−tg30o | | 1−13√3 | |
tg15o=tg( 45o−30o)= |
| = |
| =
|
| | 1+tg45o*tg30o | | 1+13√3 | |
| | 3−√3 | | (3−√3)(3−√3) | | 12−6√3 | |
= |
| = |
| = |
| =
|
| | 3+√3 | | (3+√3)(3−√3) | | 6 | |
to
r= 4√3*(2 −√3)
10 sty 05:57



 mogłabyś wyliczyć wysokość z tej metody 30,60,90 chociaż nie pamiętam o co z nią chodziło. kąt
DAC ma miarę 30 , ACD 60 (bo wysokość dzieli kąt 120 na połowę), CDA 90. I długość AC to 8
mogłabyś wyliczyć wysokość z tej metody 30,60,90 chociaż nie pamiętam o co z nią chodziło. kąt
DAC ma miarę 30 , ACD 60 (bo wysokość dzieli kąt 120 na połowę), CDA 90. I długość AC to 8
 α=30stopni
cosα=12a/b
√3/2=12a/b
a=8√3
P=12ab*sinα=12*8√3*8*12=16√3
P=12(a+2b)r
r=2Pa+2b=2*16√3/8√3+16=4√3(2−√3)
odp. r=4√3(2−√3)
My to tak zrobiliśmy a jak inna metoda zrobic prosze o pomoc
α=30stopni
cosα=12a/b
√3/2=12a/b
a=8√3
P=12ab*sinα=12*8√3*8*12=16√3
P=12(a+2b)r
r=2Pa+2b=2*16√3/8√3+16=4√3(2−√3)
odp. r=4√3(2−√3)
My to tak zrobiliśmy a jak inna metoda zrobic prosze o pomoc
 W trójkącie równoramiennym ramię ma długość 8 a kąt nachylenia ramienia do podstawy ma miarę
30stopni . Oblicz długość promienia okręgu wpisanego w ten trójkąt
Podstawa ma długość 8√3
W trójkącie równoramiennym ramię ma długość 8 a kąt nachylenia ramienia do podstawy ma miarę
30stopni . Oblicz długość promienia okręgu wpisanego w ten trójkąt
Podstawa ma długość 8√3

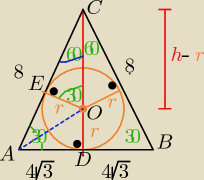 2/ sposób
h= 4 IOCI = h−r= 4−r IACI= 8 IADI = 4√3
ΔADC ~ Δ OEC z cechy ( k,k,k)
to;
2/ sposób
h= 4 IOCI = h−r= 4−r IACI= 8 IADI = 4√3
ΔADC ~ Δ OEC z cechy ( k,k,k)
to;
 miara kąta DOA = 15o bo OA zawiera się w dwusiecznej kąta 30o
to z ΔDAO mamy:
miara kąta DOA = 15o bo OA zawiera się w dwusiecznej kąta 30o
to z ΔDAO mamy: