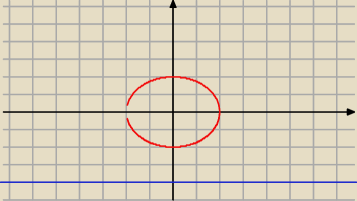
Miejsce geometryczne punktu Izunia: Dany jest okrąg o równaniu x²+y²=4 i prosta o równaniu y=−4. Wyznacz środków okręgu stycznych jednocześnie zewnętrznie do okręgu i tej prostej.

5-latek: Zrob porzadny rysunek (przeciez to geometria analityczna

Izunia: dziwne te zadanie

5-latek: Dziwna to ty jestes bo nie potrafisz nawet porzadnie przepisac zadania

Adamm:

Izunia: No tak, zobowiązująca jest Twoja nazwa użytkownika

Izunia: Ktoś wie jak to zrobić?

Janek191: Przepisz porządnie treść zadania. Tym miejscem geometrycznym środków okręgów stycznych do danego okręgu i do danej prostej będzie parabola.

5-latek: Przeciez wiadomo ze x²+y²=4 to okrag o srodku S=(0,0) i promieniu r=2 (przedszkolaki juz wiedza o tym Wspolrzedne srodka jednego okregu juz widac z rysunku S₁= (0,−3) i promien tego okregu r=1 Wez teraz cyrkiel i olowek i narysuj sobie linia przerywana okrag o srodku (0,0) i promieniu r=3 Narysuj kilka takich okregow spelniajacych warunki zadania i zobacz dokad mozna narysowac okregi o srodku na tym przerywany okregu Tak naprawde to ja nie jestem 5latek tylko 5− latek Przeczytaj sobie jeszcze raz tresc zania ktora jest tutaj napisana. Ile tych srodkow ma byc ?

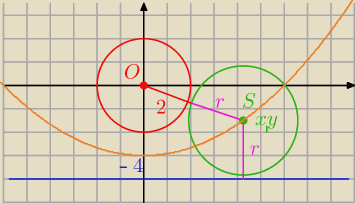
Saizou : r=|y+4| |OS|=2+r √x²+y²=2+|y+4| x²+y²=4+4|y+4|+y²+8y+16 zauważ ze y≥−3, czyli |y+4|=y+4 x²=4+4(y+4)+8y+16 x²=4y+16+8y+20 12y=x²−36

	1
y=		x2−3
	12

	1
S(x,		x2−3)
	12

piotr: (y+4+r)²=y²+x² (y+4+2)²=y²+x² ⇒

	x2
y=		−3
	12

Janek191: Brak odzewu