największa i najmniejsza wartość funkcji kk: oblicz ekstremum lokalne i wartości funkcji na krancach przedziału

	1
f(x)=		x3+x2−8x−8 , x należy <−5,3>
	3

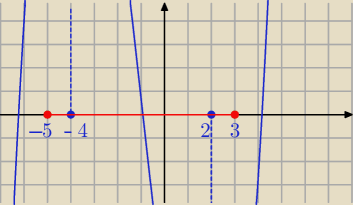Janek191: f '(x) = x² + 2 x − 8 = ( x +4)*(x − 2) = 0 ⇔ x = − 4 lub x = 2 − 4 ∊ < − 5, 3 > i 2 ∊ < − 5, 3 > f ''(x) = 2 x + 2 więc f ''( − 4) = − 6 < 0 − w punkcie x = − 4 funkcja ma maksimum lokalne y_max = f( − 4) = ... oraz f ''(2) = 6 > 0 − w punkcie x = 2 funkcja ma minimum lokalne y_min = f(2) = ... f(− 5) = U{1}{3]*(−125) + 25 + 40 − 8 = ...

	1
f(3) =		*33 + 9 − 24 − 8 = ...
	3