Rozpatrz liczbę rozwiązań równania Wiktoria: |||x+2|−4|−2|−1=m Rozpatrz liczbę rozwiązań równania . Proszę o wytłumaczenie

zef: Najwygodniej graficznie. mamy funkcję y=x+2 nakładamy na nią |f(x)| → |x+2| dajemy 4 jednostki w dół → |x+2|−4 nakładamy |f(x)| → ||x+2|−4| dajemy 2 jednostki w dół → ||x+2|−4|−2 nakładamy |f(x)| → |||x+2|−4|−2| dajemy 1 jednostkę w dół → |||x+2|−4|−2|−1 − mamy funkcję do której dążyliśmy i teraz badamy ją ze względu na parametr m który jest jakąś prostą y=m Algebraicznie byłoby dużo liczenia.

Wiktoria B: Mogłabym prosić o dokładniejsze wytłumaczenie, bo nie rozumiem do końca?

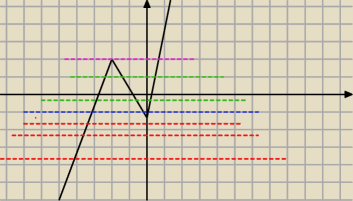
zef: Czego w tym nie rozumiesz ? Mamy przykładowy wykres funkcji m to jest prosta kolorowa W tym wykresie będzie tak 1 rozwiązanie dla m∊(−∞;−1) zauważ że dla −1 będą 2 rozwiązania (niebieska przerywana) od −1 do 2 będą 3 rozwiązania (zielona) dla 2 będą 2 rozwiązania (rózowe) i później znów będzie aż do nieskończoności 1 rozwiązanie Tak samo należy zrobić twój przykład

Wiktoria B: Skąd się wzięło y=x+2 i jak nakladac |f(x)|?

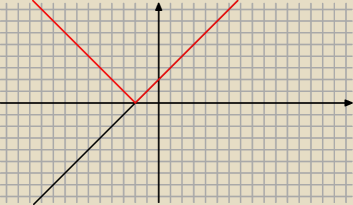
zef: y=x+2 bo zaczynam od wewnętrznej funkcji i później nią operuję nakładając wartości bezwzględne itd. nakładanie |f(x)| polega na odbiciu symetralnym wykresu znajdującego się pod osią x na górę czyli jak na rysunku: czarna linia to y=x+2 a czerwona to y=|x+2|